可持久化线段树（主席树）

Posted on | In |
Words count in article: 6.3k | Reading time ≈ 30

读以下文字时最好有些线段树的预备知识，毕竟根据发明者的原话：“想法是对原序列的每一个前缀[1..i]建立出一颗线段树维护值域上每个数的出现次数，然后发现这样的树是可以减的，然后就没有然后了”

主席树可以用来解决如下问题：“给出一列数,a1,a2…an,每次询问其中连续的一段区间ai到aj其中的第K大的数是多少？”

建那么多的线段树显然会MLE！！但是为了便于理解，这里先把这个岔放下。我们先新开一个数组t[n]，其中存着an排序并去重的值。

那么每棵线段树维护的内容是什么呢？是a1到ai这段区间中的数在t[n]中出现的次数。这段话的内容也许有点抽象，举个例子

an：4 1 1 2 8 9 4 4 3

排序并去重后得到{tn}

tn：1 2 3 4 8 9

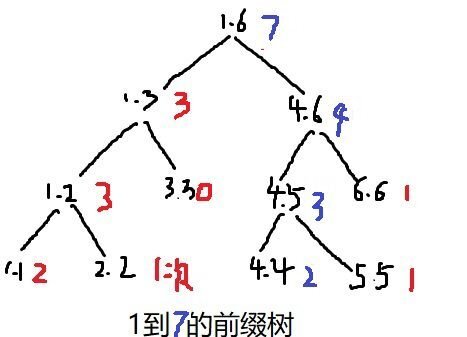
下面对前缀a[1..9]建树，它有两个1,一个2,一个3，三个4，一个8和一个9，那么它的出现次数便是线段树维护的值（为表示清楚记为Cn）建树完后如下图，树中每个节点的值表示t[i,j]中的数字在a[1..9]中出现的次数和，i，j即为节点下面标出的区间。

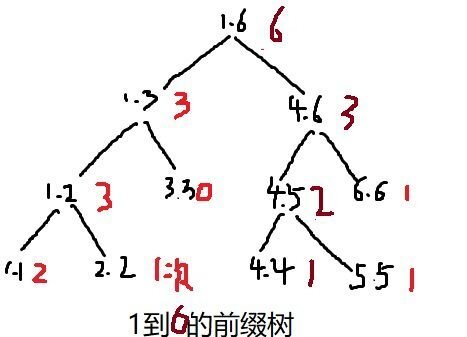
下面我们来看对于这棵树如何求第K大值。比如我们求a[1..9]中第6大的数是多少？我们看到根节点的左儿子只有4个元素，那么第6大数一定在右儿子中，并且我们可以把问题递归下去即求区间t[4,6]的三个数中为a[1..9]去除所有数字为t[1],t[2],t[3]后第2大的数是多少。（c[1]+c[2]+c[3]=4，那么6-4=2）。我们看到此时的左儿子（区间t[4,5]）有4个元素，4>2,因此第二大数一定在左儿子中，递归进入左儿子，此时即求区间t[4,5]的两个数中为a[1..9]去除所有数字为t[1],t[2],t[3],t[6]后第2大的数是多少。最后区间[4,4]有三个元素，3>2，所以第二大数一定在区间[4,4]里即t[4]=4，所以a[1..9]中第6大数为4。

这里要记住的是对于每个i , a[1,i]都有一棵树，求a[L,R]的第K大与求a[1,R]的类似，只要在每层递归时减去a[1，L-1]所在树的相应部分即可，比如在a[L,R]，小于t[mid]的数有6个，在a[1,L-1] 小于t[mid]的数有2个，那么在a[L,R] 小于t[mid]的数就有6-2=4个，递归过程和上面类似，不再详细展开。

下面解决MLE这个梗。如下图画出a1…5到9为前缀的树，然后发现树的形态都非常像！！

例子

an：4 1 1 2 8 9 4 4 3

排序并去重后得到{tn}

tn：1 2 3 4 8 9

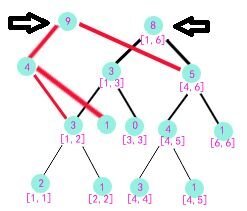
这是我们能够压缩的空间。例如以a[1..9]为前缀建的树的右子树与以a[1..8]为前缀建的树的右子树是相同的！！因此在建树a[1..9]的时候（建树是从1到9的顺序）根节点可以直接向a[1..8]的右子树连一条边。同理，对于根节点的左儿子来说（现在把这个点看做根节点），它的左子树和a[1..8]的相应部分也是相同的，因此也连一条边，如下图所示

这样我们只增加了三个点却保存了两棵树的所有信息！！像这样在前面树的基础上建树，我们只需要开一个数组储存图示两个箭头所指的根的位置就够了，顺着根向下遍历便是如前所述一棵完整的线段树

不支持修改

首先我们来了解什么叫做主席树，下面是从其他大佬的博客中复制过来的了解一下就行

所谓主席树呢，就是对原来的数列[1..n]的每一个前缀[1..i]（1≤i≤n）建立一棵线段树，线段树的每一个节点存某个前缀[1..i]中属于区间[L..R]的数一共有多少个（比如根节点是[1..n]，一共i个数，sum[root] = i；根节点的左儿子是[1..(L+R)/2]，若不大于(L+R)/2的数有x个，那么sum[root.left] = x）。若要查找[i..j]中第k大数时，设某结点x，那么x.sum[j] - x.sum[i - 1]就是[i..j]中在结点x内的数字总数。而对每一个前缀都建一棵树，会MLE，观察到每个[1..i]和[1..i-1]只有一条路是不一样的，那么其他的结点只要用回前一棵树的结点即可，时空复杂度为O(nlogn)。

看了什么的介绍，感觉并没有什么卵用，还是一脸懵逼，下面我一点一点来讲解主席树的原理以及实现过程和代码。

在学习主席树之前，需要你很熟悉线段树这个东西，因为主席树的主体是多颗线段树，首先我们来简单的回顾一下线段树的简单特点和性质，我们熟悉的线段树一般是用一个结构体表示一个节点，每个节点有一个编号，节点里面一般有两个变量l, r来表示这个节点维护的区间，然后还有一个区间信息（比如区间最大值，最小值，和等，视具体问题而定），当然如果涉及到区间更新，还有一个add或者lazy叫做延迟标记的东西，然后一般线段树最明显的特点就行，一个父节点的编号是i,那么他的两只儿子节点的编号分别为2 i(左） , 2 i + 1（右），注意主席树在这一点有别于一般的线段树，每一个父节点，他的两个儿子节点的编号不一定满足这个关系。

我们先来分析一下对于任意一个区间，我们怎样求解这个区间的第k小值，当然一个最简单的做法就是把这个区间的数都拿出来排个序，然后直接输出就好，这很简单，但是复杂度爆表，我们考虑一个线段树的做法，假如一个区间l, r我们用一个用这个区间内出现过的数的个数组成一颗线段树，这是什么意思呢，求一个区间的第k小数，当然与这个区间有多少数比他小有关，在这里我举一个例子来说明一下怎样建立这样的一颗线段树。比如这个区间表示的序列是4，1，3，2，我们要求第2小，我们一眼就看出是2，那么我们怎样上面所说的线段树来求解呢，下面我画了一幅图来讲解，其中这颗线段树上的每个节点维护的是这个节点表示区间内的个数（假设每个数都不一样）

圈内的数字表示这个区间里面有多少个数，最后叶节点表示一个数字，对应上述序列中的一个数，注意，任意一个长度为N的序列我们都可以把他离散为一个1,2,3,……,N的序列，只需要简单的hash一下就行。然后这样的一颗线段树建立出来了，我们怎样寻找区间第2小，因为叶节点从左到右表示的数依次增大，根据这个性质，以及每个节点保存了区间内的数的个数这个信息，我们可以轻易的找出区间第2小，具体的找法是，从根节点开始，看左儿子里面的数的 个数是不是大于等于2，如果是则第2小一定在左子树中，于是继续找左子树，反之找右子树，直到找到叶节点为止，然后直接返回叶节点表示的值就行。

但是多次询问区间第k小，我们每次这样建立一个线段树，这样不仅空间复杂度非常之高，而且时间复杂度也非常高，甚至比普通排序还要高，那么我们只不是可以想一个办法，使得对于每次我们查询不同的区间我们不需要重新建树，如果这样。时间复杂度和空间复杂度就大大降低了。

我们很容易就联想到了前缀和的概念，比如我们有一个问题。就是每次静态的求区间和，我们可以预处理所以的前缀和sum[i]，我们每次求解区间l, r和时，我们可以直接得到答案为sum[r] - sum[l -1],这样就不需要对区间中的每个数进行相加来求解了。

同样一个道理，我们也可以利用前缀和这个思想来解决建树这个问题，我们只需要建立n颗“前缀”线段树就行，第i树维护[1,i]序列，这样我们处理任意区间l, r时就可以通过处理区间[1,l - 1], [1,r]，就行，然后两者的处理结果进行相加相减就行。为什么满足相加减的性质，我们简单分析一下就很容易得出。如果在区间[1,l - 1]中有x个数小于一个数，在[1,r]中有y个数小于那个数，那么在区间[l,r]中就有y - x 个数小于那个数了，这样就很好理解为什么可以相加减了，另外，每颗树的结构都一样，都是一颗叶节点为n个的线段树。

上述利用前缀和的思想只是解决了时间复杂度的问题，并没有解决空间复杂度的问题，要解决空间复杂度问题。我们需要用到线段树的性质，我们每次更新一个数，那么与更新之前相比，这颗线段树改变只是一条链（从根节点到某一叶节点），那么我们可以充分利用这个特点，因为第i颗树与第i- 1颗树相比，只是更新了第i个元素，所以这两棵树有很多相同的节点，所以这两棵树可以共用很多节点（这也是为什么主席树的中节点编号不满足儿子节点编号是父节点编号的两倍和两倍加一的原因），于是这样就解决空间复杂度问题。

P3919 【模板】可持久化数组（可持久化线段树/平衡树）

手写AC（O2-1016ms）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <bits/stdc++.h>
#define N 200000+110
using namespace std;
int a[N],Hash[N],t[N],tot,n,m;
int sum[50*N],L[50*N],R[50*N];
int build(int l,int r)
{
    int rt=++tot;
    sum[rt]=0;
    if(l<r)
    {
        int m=(l+r)/2;
        L[rt]=build(l,m);
        R[rt]=build(m+1,r);
    }
    return rt;
}
int update(int pre,int l,int r,int x)
{
    int rt=++tot;
    L[rt]=L[pre];
    R[rt]=R[pre];
    sum[rt]=sum[pre]+1;
    if(l<r)
    {
        int m=(l+r)/2;
        if(x<=m)
            L[rt]=update(L[pre],l,m,x);
        else
            R[rt]=update(R[pre],m+1,r,x);
    }
    return rt;
}
int query(int u,int v,int l,int r,int k)
{
    if(l==r)
        return l;
    int num=sum[L[v]]-sum[L[u]];
    int m=(l+r)/2;
    if(num>=k)
        return query(L[u],L[v],l,m,k);
    else
        return query(R[u],R[v],m+1,r,k-num);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        Hash[i]=a[i];
    }
    sort(Hash+1,Hash+1+n);
    int d=unique(Hash+1,Hash+1+n)-Hash-1;
    t[0]=build(1,d);
    for(int i=1;i<=n;i++)
    {
        int x=lower_bound(Hash+1,Hash+1+d,a[i])-Hash;
        t[i]=update(t[i-1],1,d,x);
    }
    for(int i=1;i<=m;i++)
    {
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        int x=query(t[l-1],t[r],1,d,k);
        printf("%d\n",Hash[x]);
    }
    return 0;
}

P3567 [POI2014]KUR-Couriers

手写AC（O2-1032ms）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
#define N 500000+110
using namespace std;
int a[N],Hash[N],t[N],tot,n,m;
int sum[50*N],L[50*N],R[50*N];
int build(int l,int r)
{
    int rt=++tot;
    sum[rt]=0;
    if(l<r)
    {
        int m=(l+r)/2;
        L[rt]=build(l,m);
        R[rt]=build(m+1,r);
    }
    return rt;
}
int update(int pre,int l,int r,int x)
{
    int rt=++tot;
    L[rt]=L[pre];
    R[rt]=R[pre];
    sum[rt]=sum[pre]+1;
    if(l<r)
    {
        int m=(l+r)/2;
        if(x<=m)
            L[rt]=update(L[pre],l,m,x);
        else
            R[rt]=update(R[pre],m+1,r,x);
    }
    return rt;
}
int query(int u,int v,int l,int r,int k)
{
    if(l==r)
        return l;
    int num=sum[L[v]]-sum[L[u]];
    int num1=sum[R[v]]-sum[R[u]];
    int m=(l+r)/2;
    if(num>=k)
        return query(L[u],L[v],l,m,k);
    else if(num1>=k)
        return query(R[u],R[v],m+1,r,k);
    else
        return 0;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        Hash[i]=a[i];
    }
    sort(Hash+1,Hash+1+n);
    int d=unique(Hash+1,Hash+1+n)-Hash-1;
    t[0]=build(1,d);
    for(int i=1;i<=n;i++)
    {
        int x=lower_bound(Hash+1,Hash+1+d,a[i])-Hash;
        t[i]=update(t[i-1],1,d,x);
    }
    for(int i=1;i<=m;i++)
    {
        int l,r,k;
        scanf("%d%d",&l,&r);
        k=(r-l+1)/2+1;
        int x=query(t[l-1],t[r],1,d,k);
        printf("%d\n",Hash[x]);
    }
    return 0;
}

HDU 4417 Super Mario

纯手写AC（140ms）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <bits/stdc++.h>
#define N 500000+110
#define inf 2147483647
using namespace std;
int a[N],Hash[N];
int sum[50*N],L[50*N],R[50*N],t[N],tot,n,m;
int build(int l,int r)
{
    int rt=++tot;
    sum[rt]=0;
    if(l<r)
    {
        int m=(l+r)/2;
        L[rt]=build(l,m);
        R[rt]=build(m+1,r);
    }
    return rt;
}
int update(int pre,int l,int r,int x)
{
    int rt=++tot;
    L[rt]=L[pre];
    R[rt]=R[pre];
    sum[rt]=sum[pre]+1;
    if(l<r)
    {
        int m=(l+r)/2;
        if(x<=m)
            L[rt]=update(L[pre],l,m,x);
        else
            R[rt]=update(R[pre],m+1,r,x);
    }
    return rt;
}
int query(int u,int v,int l,int r,int k)
{
    if(l==r)
        return sum[v]-sum[u];
    int b=0;
    int m=(l+r)/2;
    if(k>m)
    {
        b+=sum[L[v]]-sum[L[u]];
        b+=query(R[u],R[v],m+1,r,k);
    }
    else
        b+=query(L[u],L[v],l,m,k);
    return b;
}
int main()
{
    int T;
    scanf("%d",&T);
    for(int j=1;j<=T;j++)
    {
        tot=0;
        printf("Case %d:\n",j);
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
        {
            scanf("%lld",&a[i]);
            Hash[i]=a[i];
        }
        sort(Hash+1,Hash+1+n);
        int d=unique(Hash+1,Hash+1+n)-Hash-1;
        Hash[++d]=inf;
        t[0]=build(1,d);
        for(int i=1;i<=n;i++)
        {
            int x=lower_bound(Hash+1,Hash+1+d,a[i])-Hash;
            t[i]=update(t[i-1],1,d,x);
        }
        for(int i=1;i<=m;i++)
        {
            int l,r;
            long long h;
            scanf("%d%d%lld",&l,&r,&h);
            l++;
            r++;
            int ans=0;
            int k=upper_bound(Hash+1,Hash+1+d,h)-Hash-1;
            if(k>0)
                ans=query(t[l-1],t[r],1,d,k);
            printf("%d\n",ans);
        }
    }
    return 0;
}

带修改（主席树+树状数组）

P2617 Dynamic Rankings

题意：n个数，q个询问 (n<=50000, q<=10000)

Q x y z 代表询问[x, y]区间里的第z小的数

C x y 代表将(从左往右数)第x个数变成y

上篇介绍了在[x, y]区间内查询第z小的数的方法(静态主席树)

本题有更新操作

若仍用上篇的做法，每次更新一个数，需要更新的是T[i], T[i+1]… …Tn，因为每棵树T[i]所记录的都是前缀(1到i的数出现的次数) 因此，改变i，会影响i到n的所有树

这样，每次更新的复杂度最坏为O(nn)，最坏更新q次即为O(n×mn×m) 复杂度相当庞大，很明显这样做是不行的

那怎么办呢？

我们可以发现，对于改变i处的数这个操作，对于T[i], T[i+1]… …T[n]这些树的影响是相同的，都只改变了 “原来i处的数 的数量” 和 “现在i处的数 的数量” 这两个值而已，我们只要在原来的基础上增加一类树， 用它们来维护更新掉的数，即用树状数组来记录更新，每次更新lognlogn棵树。

下面来演示一下建树到查询的过程：

比如此题的第一个案例

5 33 2 1 4 7

Q 1 4 3

C 2 6

Q 2 5 3

先将序列以及要更新的数(C操作)离散化

即3 2 1 4 7 、 6 ——>(排序) ——> 1 2 3 4 6 7

那么我们就需要建一棵这样的树：

(圈里的都是结点的编号， 4、5、6、9、10、11号结点代表的分别是1、2、3、4、6、7)

(4、5、9、10你也可以任意作为6或11的儿子， 递归生成的是类似这样的， 这并不重要)

对于3 2 1 4 7(先不管需要更新的6)建完树见下图(建树过程同静态的，不明白的请向上翻)

(红色的是个数， 相同结点的个数省略了，同前一棵树)

对于C操作之前的Q，就跟静态的类似，减一减 找就好了

然后下面要更新了

对于更新， 我们不改变这些已经建好的树， 而是另建一批树S，用来记录更新，而这批线段树，我们用树状数组来维护

也就是树状数组的每个节点都是一颗线段树

一开始，S[0]、S[1]、S[2]、S[3]、S[4]、S5这些都与T[0]相同(也就是每个节点建了一棵空树)

对于C 2 6 这个操作， 我们只需要减去一个2，加上一个6即可

对于减去2

(树状数组i+lowbit(i)为i的父亲节点， 修改i，就要把i的所有父亲节点都修改了)

2在树状数组中出现的位置是 2、2+lowbit(2)=4 这两个位置，

因此要更新的是S[2]和S[4]这两个节点中的树

删去2后是这样

加上一个6 (同样是对于2号位置， 因此需要更新的仍是S[2]和S[4])

加上之后是这样

当查询的时候， 对树T的操作与静态的一致，另外再加上S树的值就好了

教练的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <cmath>
#define N 60000+5//空间为nlogn*logn
using namespace std;

struct node
{
    int l;
    int r;
    int flag;
    int k;
}q[N];
int a[N],Hash[2*N],L[32*N],R[32*N],sum[32*N],s[32*N],T[32*N],n,m,dd,tot,use[32*N];
int lowbit(int x){return x&(-x);}
int getsum(int x)
{
    int ret=0;
    while(x>0)
    {
        ret+=sum[L[use[x]]];
        x-=lowbit(x);
    }
    return ret;
}
int build(int l,int r)
{
    int rt=++tot;
    int m=(l+r)/2;
    if(l<r)
    {
        L[rt]=build(l,m);
        R[rt]=build(m+1,r);
    }
    return rt;
}
int update(int pre,int l,int r,int x,int d)
{
    int rt=++tot;
    L[rt]=L[pre];R[rt]=R[pre];sum[rt]=sum[pre]+d;
    if(l<r)
    {
        int m=(l+r)/2;
        if(x<=m)
            L[rt]=update(L[pre],l,m,x,d);
        else
            R[rt]=update(R[pre],m+1,r,x,d);
    }
    return rt;
}
int query(int u,int v,int ll,int rr,int l,int r,int k)
{
    if(l>=r)return l;
    int m=(l+r)/2;
    int aa=getsum(v);
    int bb=getsum(u);
    int num=aa-bb+sum[L[rr]]-sum[L[ll]];
    if(k<=num)
    {
        for(int j=u;j>0;j=j-lowbit(j))use[j]=L[use[j]];
        for(int j=v;j>0;j=j-lowbit(j))use[j]=L[use[j]];
        return query(u,v,L[ll],L[rr],l,m,k);
    }
    else
    {
        for(int j=u;j>0;j=j-lowbit(j))use[j]=R[use[j]];
        for(int j=v;j>0;j=j-lowbit(j))use[j]=R[use[j]];
        return query(u,v,R[ll],R[rr],m+1,r,k-num);
    }
}
void modify(int x,int p,int d)
{
    while(x<=n)
    {
        s[x]=update(s[x],1,dd,p,d);
        x+=lowbit(x);
    }
}
int main()
{
    scanf("%d %d",&n,&m);
    int d=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        Hash[++d]=a[i];
    }
    char ss[5];
    for(int i=1;i<=m;i++)
    {
        scanf("%s",ss);
        if(ss[0]=='Q')
        {
            scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].k);
            q[i].flag=1;
        }
        else
        {
            scanf("%d%d",&q[i].l,&q[i].r);
            Hash[++d]=q[i].r;
            q[i].flag=0;
        }
    }
    sort(Hash+1,Hash+1+d);
    dd=unique(Hash+1,Hash+1+d)-Hash-1;
    T[0]=build(1,dd);
    for(int i=1;i<=n;i++)
    {
        int x=lower_bound(Hash+1,Hash+1+dd,a[i])-Hash;
        T[i]=update(T[i-1],1,dd,x,1);
    }
    for(int i=1;i<=n;i++)s[i]=T[0];
    for(int i=1;i<=m;i++)
    {
        if(q[i].flag)
        {
            for(int j=q[i].l-1;j>0;j=j-lowbit(j))use[j]=s[j];
            for(int j=q[i].r;j>0;j=j-lowbit(j))use[j]=s[j];
            int t=query(q[i].l-1,q[i].r,T[q[i].l-1],T[q[i].r],1,dd,q[i].k);
            printf("%d\n",Hash[t]);
        }
        else
        {
            int xx=lower_bound(Hash+1,Hash+1+dd,a[q[i].l])-Hash;
            int yy=lower_bound(Hash+1,Hash+1+dd,q[i].r)-Hash;
            modify(q[i].l,xx,-1);
            modify(q[i].l,yy,1);
            a[q[i].l]=q[i].r;
        }
    }
    return 0;
}

手写AC（对拍O2-96ms）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
#include <bits/stdc++.h>
#define N 60010
using namespace std;
struct node
{
    int l,r,flag,k;
};struct node q[N];
int a[N],Hash[2*N],L[32*N],R[32*N],sum[32*N],s[32*N],T[32*N],n,m,dd,tot,use[32*N];
inline int lowbit(int x)
{
    return x&(-x);
}
inline int getsum(int x)
{
    int ret=0;
    while(x>0)
    {
        ret+=sum[L[use[x]]];
        x-=lowbit(x);
    }
    return ret;
}
inline int build(int l,int r)
{
    int rt=++tot;
    int m=(l+r)>>1;
    if(l<r)
    {
        L[rt]=build(l,m);
        R[rt]=build(m+1,r);
    }
    return rt;
}
inline int update(int pre,int l,int r,int x,int d)
{
    int rt=++tot;
    L[rt]=L[pre];
    R[rt]=R[pre];
    sum[rt]=sum[pre]+d;
    if(l<r)
    {
        int m=(l+r)>>1;
        if(x<=m)
            L[rt]=update(L[pre],l,m,x,d);
        else
            R[rt]=update(R[pre],m+1,r,x,d);
    }
    return rt;
}
inline int query(int u,int v,int left,int right,int l,int r,int k)
{
    if(l>=r)
        return l;
    int m=(l+r)>>1;
    int aa=getsum(v);
    int bb=getsum(u);
    int num=aa-bb+sum[L[right]]-sum[L[left]];
    if(k<=num)
    {
        for(register int j=u;j>0;j-=lowbit(j))
            use[j]=L[use[j]];
        for(register int j=v;j>0;j-=lowbit(j))
            use[j]=L[use[j]];
        return query(u,v,L[left],L[right],l,m,k);
    }
    else
    {
        for(register int j=u;j>0;j-=lowbit(j))
            use[j]=R[use[j]];
        for(register int j=v;j>0;j-=lowbit(j))
            use[j]=R[use[j]];
        return query(u,v,R[left],R[right],m+1,r,k-num);
    }
}
inline void modify(int x,int p,int d)
{
    while (x<=n)
    {
        s[x]=update(s[x],1,dd,p,d);
        x+=lowbit(x);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    int d=0;
    for(register int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        Hash[++d]=a[i];
    }
    char ss[5];
    for(register int i=1;i<=m;i++)
    {
        scanf("%s",ss);
        if(ss[0]=='Q')
        {
            scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].k);
            q[i].flag=1;
        }
        else
        {
            scanf("%d%d",&q[i].l,&q[i].r);
            Hash[++d]=q[i].r;
            q[i].flag=0;
        }
    }
    sort(Hash+1,Hash+1+d);
    dd=unique(Hash+1,Hash+1+d)-Hash-1;
    T[0]=build(1,dd);
    for(register int i=1;i<=n;i++)
    {
        int x=lower_bound(Hash+1,Hash+1+dd,a[i])-Hash;
        T[i]=update(T[i-1],1,dd,x,1);
    }
    for(register int i=1;i<=n;i++)
        s[i]=T[0];
    for(register int i=1;i<=m;i++)
    {
        if(q[i].flag)
        {
            for(register int j=q[i].l-1;j>0;j-=lowbit(j))
                use[j]=s[j];
            for(register int j=q[i].r;j>0;j-=lowbit(j))
                use[j]=s[j];
            int t=query(q[i].l-1,q[i].r,T[q[i].l-1],T[q[i].r],1,dd,q[i].k);
            printf("%d\n",Hash[t]);
        }
        else
        {
            int xx=lower_bound(Hash+1,Hash+1+dd,a[q[i].l])-Hash;
            int yy=lower_bound(Hash+1,Hash+1+dd,q[i].r)-Hash;
            modify(q[i].l,xx,-1);
            modify(q[i].l,yy,1);
            a[q[i].l]=q[i].r;
        }
    }
    return 0;
}

例题

P1383 高级打字机

手写AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <bits/stdc++.h>
#define N 500010
using namespace std;
int a[N*32],L[32*N],R[32*N],sum[32*N],T[32*N],n,m,tot,cnt,use[32*N],root[32*N];
inline int Insert(int pre,int l,int r,int p,int x)
{
    int rt=++tot;
    if(l==r)
    {
        a[rt]=x;
        sum[rt]=sum[pre]+1;
        return rt;
    }
    L[rt]=L[pre];
    R[rt]=R[pre];
    sum[rt]=sum[pre]+1;
    int m=(l+r)>>1;
    if(p<=m)
        L[rt]=Insert(L[pre],l,m,p,x);
    else
        R[rt]=Insert(R[pre],m+1,r,p,x);
    return rt;
}
inline int build(int l,int r)
{
    int rt=++tot;
    int m=(l+r)>>1;
    if(l<r)
    {
        L[rt]=build(l,m);
        R[rt]=build(m+1,r);
    }
    return rt;
}
inline int query(int p,int l,int r,int x)
{
    if(l==r)
        return a[p];
    int m=(l+r)>>1;
    if(x<=sum[L[p]])
        return query(L[p],l,m,x);
    else
        return query(R[p],m+1,r,x-sum[L[p]]);
}
int main()
{
    scanf("%d",&n);
    root[0]=build(1,n);
    char ss[5];
    for(register int i=1;i<=n;i++)
    {
        scanf("%s",ss);
        if(ss[0]=='T')
        {
            char ch;
            scanf("%s",&ch);
            int x=ch-'a'+1;
            root[++cnt]=Insert(root[cnt-1],1,n,i,x);
        }
        else if(ss[0]=='U')
        {
            int x;
            scanf("%d",&x);
            root[++cnt]=root[cnt-x-1];
        }
        else
        {
            int x;
            scanf("%d",&x);
            char ch=query(root[cnt],1,n,x)+'a'-1;
            printf("%c\n",ch);
        }
    }
    return 0;
}

0%