莫队

Posted on | In |
Words count in article: 5.2k | Reading time ≈ 28

%一波莫涛队长orz

普通莫队

由于没有什么板子，这里放一道基础题。

给定一个序列，其中有n个元素，有m次查询，每次查询要求输出区间[l,r]内出现次数不少于k的数字的个数。

其实乍一看，好像就是可以用暴力做……但其实莫队本身也和暴力区别不大，基础思路就是将序列分成sqrt(n)个块，然后在每个块中进行操作。

以下是代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
#define N 100000+100
using namespace std;
struct node
{
    int l,r,k,id,t;
}ask[N];
int n,m,blo,a[N],num[N],ans[N],cnt[N];
inline bool cmp(node x,node y)
{
    if(x.t==y.t)
        return x.r<y.r;
    return x.t<y.t;
}
inline void add(int x)
{
    num[a[x]]++;
    cnt[num[a[x]]]++;
}
inline void Minus(int x)
{
    num[a[x]]--;
    cnt[num[a[x]]]--;
}
int main()
{
    scanf("%d%d",&n,&m);
    blo=sqrt(n);
    for(register int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    for(register int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&ask[i].l,&ask[i].r,&ask[i].k);
        ask[i].id=i;
        ask[i].t=ask[i].l/blo;
    }
    sort(ask+1,ask+1+m,cmp);
    for(register int i=ask[1].l;i<=ask[1].r;i++)
    {
        num[a[i]]++;
        cnt[num[a[i]]]++;
    }
    ans[ask[1].id]=cnt[ask[1].k];
    int L=ask[1].l;
    int R=ask[1].r;
    for(register int i=2;i<=m;i++)
    {
        while(L>ask[i].l)
        {
            L--;
            add(L);
        }
        while(R<ask[i].r)
        {
            R++;
            add(R);
        }
        while(L<ask[i].l)
        {
            Minus(L);
            L++;
        }
        while(R>ask[i].r)
        {
            Minus(R);
            R--;
        }
        ans[ask[i].id]=cnt[ask[i].k];
    }
    for(register int i=1;i<=m;i++)
        printf("%d\n",ans[i]);
    return 0;
}

在这个程序中，我们用num[j]来记录j的出现次数，用cnt[j]记录出现次数不小于j的数的个数，在离线操作的基础上，对每次查询依照左端点所在的块进行排序，如果所在块相同则按照右端点进行排序，可以保证L，R两个指针的跳动次数尽可能的小以降低复杂度。

然后在对每次查询的更新中不断跳动L、R，拓宽区间的时候先拓宽再操作，缩小区间的时候则先操作再缩小，最终在记录下来的ans数组中查询答案。

以下是几道题：

BZOJ 3809: Gty的二逼妹子序列

手写AC（调了一下午的绝望）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <bits/stdc++.h>
#define N 1000000+1000
using namespace std;
int n,m,blo,cnt;
int a[100005],ans[1000005];
int bel[100005];
int num[100005],bloans[1005];
struct node
{
	int l,r,p,q,id;
}ask[1000005];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch>'9'||ch<'0')
    {
        if(f=='-')
            f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline bool cmp(node x,node y)
{
    if(bel[x.l]==bel[y.l])
        return x.r<y.r;
    return bel[x.l]<bel[y.l];
}
inline void add(int x)
{
    num[a[x]]++;
    if(num[a[x]]==1)
        bloans[bel[a[x]]]++;
}
inline void Minus(int x)
{
    num[a[x]]--;
    if(!num[a[x]])
        bloans[bel[a[x]]]--;
}
inline int query(int x,int y)
{
	int ret=0;
	int L=bel[x];
    int R=bel[y];
	if(L==R)
	{
        for(register int i=x;i<=y;i++)
		{
            if(num[i])
                ret++;
        }
    }
	else
	{
		for(register int i=x;i<(L+1)*blo;i++)
		{
            if(num[i])
                ret++;
        }
		for(register int i=R*blo;i<=y;i++)
		{
            if(num[i])
                ret++;
        }
        for(register int i=L+1;i<R;i++)
    		ret+=bloans[i];
	}
	return ret;
}
int main()
{
    n=read();
    m=read();
    blo=sqrt(n);
    for(register int i=1;i<=n;i++)
    {
        a[i]=read();
        bel[i]=i/blo;
    }
    for(register int i=1;i<=m;i++)
    {
        ask[i].l=read();
        ask[i].r=read();
        ask[i].p=read();
        ask[i].q=read();
        ask[i].id=i;
    }
    sort(ask+1,ask+1+m,cmp);
    int L=1;
    int R=0;
    for(register int i=1;i<=m;i++)
    {
        while(L>ask[i].l)
        {
            L--;
            add(L);
        }
        while(R<ask[i].r)
        {
            R++;
            add(R);
        }
        while(L<ask[i].l)
        {
            Minus(L);
            L++;
        }
        while(R>ask[i].r)
        {
            Minus(R);
            R--;
        }
        ans[ask[i].id]=query(ask[i].p,ask[i].q);
    }
    for(register int i=1;i<=m;i++)
        printf("%d\n",ans[i]);
    return 0;
}

这道题说起来难度其实不大，一个值域分块的莫队保证m√n的复杂度完全没压力，就是这个28Mb的空间稍微有点坑。

P4137 Rmq Problem / mex

手写AC（一遍A O2-1296ms）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>
#define N 200000+1000
using namespace std;
struct node
{
    int l,r,id;
}ask[N];
int n,m,blo,now,a[N],num[N],ans[N],bel[N];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch>'9'||ch<'0')
    {
        if(f=='-')
            f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline bool cmp(node x,node y)
{
    if(bel[x.l]==bel[y.l])
        return x.r<y.r;
    return bel[x.l]<bel[y.l];
}
inline void add(int x)
{
    if(a[x]>n)
        return;
    num[a[x]]++;
    if(a[x]==now)
    {
        while(num[now])
            now++;
    }
}
inline void Minus(int x)
{
    if(a[x]>n)
        return;
    num[a[x]]--;
    if(a[x]<now)
        if(!num[a[x]])
            now=a[x];
}
int main()
{
    n=read();
    m=read();
    blo=sqrt(n);
    for(register int i=1;i<=n;i++)
    {
        a[i]=read();
        bel[i]=i/blo;
    }
    for(register int i=1;i<=m;i++)
    {
        ask[i].l=read();
        ask[i].r=read();
        ask[i].id=i;
    }
    sort(ask+1,ask+1+m,cmp);
    int L=1;
    int R=0;
    for(register int i=1;i<=m;i++)
    {
        while(L>ask[i].l)
        {
            L--;
            add(L);
        }
        while(R<ask[i].r)
        {
            R++;
            add(R);
        }
        while(L<ask[i].l)
        {
            Minus(L);
            L++;
        }
        while(R>ask[i].r)
        {
            Minus(R);
            R--;
        }
        ans[ask[i].id]=now;
    }
    for(register int i=1;i<=m;i++)
        printf("%d\n",ans[i]);
    return 0;
}

仍旧是对0到n进行分块，因为最坏情况是a[1]~a[n]对应0~n-1。所以就在上一题的基础上修改一下更新操作，在每次更新的时候与当前的最小值进行比较，如果最小值数量增加就寻找新的最优解，如果有新的解出现并且优于最优解就更新最优解。

BZOJ 3236: [AHOI2013]作业

手写AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#include <bits/stdc++.h>
#define N 1000000+1000
using namespace std;
int n,m,blo,cnt;
int a[100005],ans[1000005][2];
int bel[100005];
int num[100005],bloans[1005],bloans1[1005];
struct node
{
    int l,r,p,q,id;
}ask[1000005];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch>'9'||ch<'0')
    {
        if(f=='-')
            f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline bool cmp(node x,node y)
{
    if(bel[x.l]==bel[y.l])
        return x.r<y.r;
    return bel[x.l]<bel[y.l];
}
inline void add(int x)
{
    num[a[x]]++;
    bloans1[bel[a[x]]]++;
    if(num[a[x]]==1)
        bloans[bel[a[x]]]++;
}
inline void Minus(int x)
{
    num[a[x]]--;
    bloans1[bel[a[x]]]--;
    if(!num[a[x]])
        bloans[bel[a[x]]]--;
}
inline int query(int x,int y)
{
    int ret=0;
    int L=bel[x];
    int R=bel[y];
    if(L==R)
    {
        for(register int i=x;i<=y;i++)
        {
            if(num[i])
                ret++;
        }
    }
    else
    {
        for(register int i=x;i<(L+1)*blo;i++)
        {
            if(num[i])
                ret++;
        }
        for(register int i=R*blo;i<=y;i++)
        {
            if(num[i])
                ret++;
        }
        for(register int i=L+1;i<R;i++)
            ret+=bloans[i];
    }
    return ret;
}
inline int Query(int x,int y)
{
    int ret=0;
    int L=bel[x];
    int R=bel[y];
    if(L==R)
    {
        for(register int i=x;i<=y;i++)
            ret+=num[i];
    }
    else
    {
        for(register int i=x;i<(L+1)*blo;i++)
            ret+=num[i];
        for(register int i=R*blo;i<=y;i++)
            ret+=num[i];
        for(register int i=L+1;i<R;i++)
            ret+=bloans1[i];
    }
    return ret;
}
int main()
{
    n=read();
    m=read();
    blo=sqrt(n);
    for(register int i=1;i<=n;i++)
    {
        a[i]=read();
        bel[i]=i/blo;
    }
    for(register int i=1;i<=m;i++)
    {
        ask[i].l=read();
        ask[i].r=read();
        ask[i].p=read();
        ask[i].q=read();
        ask[i].id=i;
    }
    sort(ask+1,ask+1+m,cmp);
    int L=1;
    int R=0;
    for(register int i=1;i<=m;i++)
    {
        while(L>ask[i].l)
        {
            L--;
            add(L);
        }
        while(R<ask[i].r)
        {
            R++;
            add(R);
        }
        while(L<ask[i].l)
        {
            Minus(L);
            L++;
        }
        while(R>ask[i].r)
        {
            Minus(R);
            R--;
        }
        ans[ask[i].id][0]=query(ask[i].p,ask[i].q);
        ans[ask[i].id][1]=Query(ask[i].p,ask[i].q);
    }
    for(register int i=1;i<=m;i++)
        printf("%d %d\n",ans[i][1],ans[i][0]);
    return 0;
}

几乎无思维难度，在BZOJ 3809的基础上加一个查询数量的函数就行了

带修莫队

P1903 [国家集训队]数颜色

手写AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
#include <bits/stdc++.h>
#define N 100000+100
using namespace std;
int n,m,blo,cnt,t,Time;
int a[N],ans[N],bel[N],num[N],bloans[N],now[N];
struct node
{
    int l,r,tim,id;
}ask[N];
struct change
{
    int pos,New,Old;
}chg[N];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch>'9'||ch<'0')
    {
        if(f=='-')
            f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline bool cmp(node x,node y)
{
    if(bel[x.l]==bel[y.l])
    {
        if(bel[x.r]==bel[y.r])
            return x.tim<y.tim;
        return bel[x.r]<bel[y.r];
    }
    return bel[x.l]<bel[y.l];
}
inline void add(int x)
{
    num[x]++;
    if(num[x]==1)
        cnt++;
}
inline void Minus(int x)
{
    num[x]--;
    if(!num[x])
        cnt--;
}
inline void Change(int l,int r,int x,int d)
{
    if(l<=x&&x<=r)
    {
        add(d);
        Minus(a[x]);
    }
    a[x]=d;
}
int main()
{
    n=read();
    m=read();
    blo=pow(n,2.0/3);
    for(register int i=1;i<=n;i++)
    {
        a[i]=read();
        now[i]=a[i];
        bel[i]=i/blo;
    }
    for(register int i=1;i<=m;i++)
    {
        char ch;
        cin>>ch;
        if(ch=='Q')
        {
            ask[++t].l=read();
            ask[t].r=read();
            ask[t].tim=Time;
            ask[t].id=t;
        }
        else
        {
            chg[++Time].pos=read();
            chg[Time].New=read();
            chg[Time].Old=now[chg[Time].pos];
            now[chg[Time].pos]=chg[Time].New;
        }
    }
    sort(ask+1,ask+1+t,cmp);
    int L=1;
    int R=0;
    int T=0;
    for(register int i=1;i<=t;i++)
    {
        while(T<ask[i].tim)
        {
            T++;
            Change(L,R,chg[T].pos,chg[T].New);
        }
        while(T>ask[i].tim)
        {
            Change(L,R,chg[T].pos,chg[T].Old);
            T--;
        }
        while(L>ask[i].l)
        {
            L--;
            add(a[L]);
        }
        while(R<ask[i].r)
        {
            R++;
            add(a[R]);
        }
        while(L<ask[i].l)
        {
            Minus(a[L]);
            L++;
        }
        while(R>ask[i].r)
        {
            Minus(a[R]);
            R--;
        }
        ans[ask[i].id]=cnt;
    }
    for(register int i=1;i<=t;i++)
        printf("%d\n",ans[i]);
    return 0;
}

就难度系数而言其实并不算高，作为带修莫队的板子题来说挺不错的。

那么以下是带修莫队的思路。

如果我们把每次修改当作一次时间的推移，然后就只需要在查询中加入一个新的关键字Tim，也就是时间，仅在两个询问的l和r都在同一分块中的情况才依照Tim进行排序。

然后在操作中进行L和R的跳动之前先进行时间指针T的跳动，使时间到达当前查询的时间点。由于时间需要不停的跳动，所以对于每次修改操作要另开一个结构体记录修改位置（pos）、修改后的值（New）和修改前的值（Old），这个Old在后面时间倒流的时候会有用。

对于每次T的跳动进行一次Change操作，时间增加就将指定位置的值修改为T++后的修改操作的New值，时间倒流就先将指定位置的值修改为T时修改操作的Old值（即还原），然后就没什么区别了。

对于Change操作也比较简单，如果当前位置在[L,R]区间中就将修改后的值Add进去，然后将原位置上的值Minus掉，如果不在区间内就直接将原位置数据赋为修改后的值，因为以后指针跳动的时候会自行更新的。

稍微扯两句，带修莫队的复杂度经过某些dalao的证明后确定为n^(5/3),此时分为n^(1/3)块，每块有n^(2/3)个元素，所以blo=pow(n,2.0/3)。

树上莫队

例题：BZOJ 4129: Haruna’s Breakfast（小天使！！！！！！！！）

什么，树上能跑莫队，还带修改？那岂不是要爆裂吗？

这是我第一次听说树上莫队时的想法。

不过我们知道对于一棵树，还有DFS序这种美妙的东西，这样的话树不就变成序列了吗？

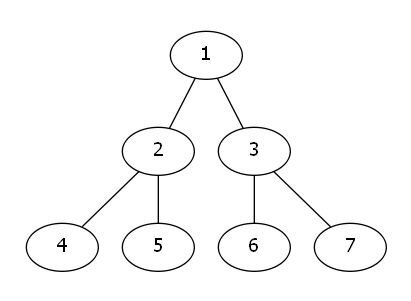
比如说对于下面一棵树：

它的DFS序就是：1 2 4 4 5 5 2 3 6 6 7 7 3 1

然后求j,k两点之间的链上的mex值。我们用in[i]记录i第一次出现的位置，用out[i]记录i最后出现的位置。

首先假设j是k的祖先，那么我们可以发现[j,k]间的信息就存在in[j],in[k]之间或out[j],out[k]之间，对于出现两次的数我们就忽略掉好了。

那么如果j不是k的祖先呢？我们会发现[j,k]之间的信息存在了in[j],out[k]之间或者out[j],in[k]之间，同样我们忽略出现了两次的数。但是如果仔细看一下就会发现，j、k的LCA好像不见了，那么我们只要特殊处理一下LCA就OK了。

然后就可以用序列上的莫队来处理了DA☆ZE！（不过代码比较长就是了）

以下是AC代码（我可是自带大常数和大空间的男人）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
#include <bits/stdc++.h>
#define N 500000+100
using namespace std;
int n,m,blo,cnt,Time,tot,cur;
int a[N],in[N],dfn[N],ans[N],bel[N],num[N],out[N],now[N];
int siz[N],deep[N],fa[N],son[N],p[N],top[N];
short tag[N];
struct node
{
    int l,r,tim,id,Lca;
}ask[N];
struct change
{
    int pos,New,Old;
}chg[N];
struct edge
{
    int to,nxt;
}e[N];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch>'9'||ch<'0')
    {
        if(f=='-')
            f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline bool cmp(node x,node y)
{
    if(bel[x.l]==bel[y.l])
    {
        if(bel[x.r]==bel[y.r])
            return x.tim<y.tim;
        return bel[x.r]<bel[y.r];
    }
    return bel[x.l]<bel[y.l];
}
inline void add_edge(int u,int v)
{
    e[++tot]=(edge){v,p[u]};
    p[u]=tot;
}
inline void dfs(int x)
{
    siz[x]++;
    dfn[++dfn[0]]=x;
    in[x]=dfn[0];
    int f=-1;
    for(int i=p[x];i;i=e[i].nxt)
    {
        int v=e[i].to;
        if(v==fa[x])
            continue;
        deep[v]=deep[x]+1;
        fa[v]=x;
        dfs(v);
        siz[x]+=siz[v];
        if(siz[v]>f)
        {
            son[x]=v;
            f=siz[v];
        }
    }
    if(f==-1)
        son[x]=x;
    dfn[++dfn[0]]=x;
    out[x]=dfn[0];
}
inline int LCA(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(deep[top[x]]<deep[top[y]])
            swap(x,y);
        x=fa[top[x]];
    }
    if(deep[x]>deep[y])
        swap(x,y);
    return x;
}
inline void choose(int x,int y,int cur)
{
    int l=0,r=0,lca=LCA(x,y);
    if(x==lca||y==lca)
    {
        if(abs(in[x]-in[y])<abs(out[x]-out[y]))
            l=min(in[x],in[y]),r=max(in[x],in[y]);
        else
            l=min(out[x],out[y]),r=max(out[x],out[y]);
        lca=0;
    }
    else
    {
        if(abs(in[x]-out[y])<abs(out[x]-in[y]))
            l=min(in[x],out[y]),r=max(in[x],out[y]);
        else
            l=min(out[x],in[y]),r=max(out[x],in[y]);
    }
    ask[cur]=(node){l,r,Time,cur,lca};
}
inline void add(int x)
{
    if(x>n)
        return;
    num[x]++;
    if(x==cnt)
    {
        while(num[cnt])
            cnt++;
    }
}
inline void Minus(int x)
{
    if(x>n)
        return;
    num[x]--;
    if(x<cnt)
        if(!num[x])
            cnt=x;
}
inline void Work(int x)
{
    if(tag[x])
        Minus(a[x]);
    else
        add(a[x]);
    tag[x]^=1;
}
inline void Change(int pos,int x)
{
    if(tag[pos])
    {
        Work(pos);
        a[pos]=x;
        Work(pos);
    }
    else
        a[pos]=x;
}
int main()
{
    n=read(),m=read();
    blo=pow(n<<1,2.0/3)*0.7;
    for(register int i=1;i<=n;i++)
        now[i]=a[i]=read();
    for(register int i=1;i<n;i++)
    {
        int x,y;
        x=read(),y=read();
        add_edge(x,y),add_edge(y,x);
    }
    dfs(1);
    for(register int i=1;i<=dfn[0];i++)
    {
        bel[i]=i/blo;
        if(top[dfn[i]])
            continue;
        else if(dfn[i]==son[fa[dfn[i]]])
            top[dfn[i]]=top[fa[dfn[i]]];
        else
            top[dfn[i]]=dfn[i];
    }
    for(register int i=1;i<=m;i++)
    {
        int c=read();
        if(c)
        {
            int x=read(),y=read();
            choose(x,y,++cur);
        }
        else
        {
            int x=read(),y=read();
            chg[++Time]=(change){x,y,now[x]};
            now[x]=y;
        }
    }
    sort(ask+1,ask+1+cur,cmp);
    int L=1,R=0,T=0;
    for(register int i=1;i<=cur;i++)
    {
        while(T<ask[i].tim)
        {
            T++;
            Change(chg[T].pos,chg[T].New);
        }
        while(T>ask[i].tim)
        {
            Change(chg[T].pos,chg[T].Old);
            T--;
        }
        while(L>ask[i].l)
        {
            L--;
            Work(dfn[L]);
        }
        while(R<ask[i].r)
        {
            R++;
            Work(dfn[R]);
        }
        while(L<ask[i].l)
        {
            Work(dfn[L]);
            L++;
        }
        while(R>ask[i].r)
        {
            Work(dfn[R]);
            R--;
        }
        if(ask[i].Lca)
            Work(ask[i].Lca);
        ans[ask[i].id]=cnt;
        if(ask[i].Lca)
            Work(ask[i].Lca);
    }
    for(register int i=1;i<=cur;i++)
        printf("%d\n",ans[i]);
    return 0;
}

这里LCA我用的树剖（当然倍增也可以啦

顺便注明一下，那个tag数组是用来记录某个位置在区间里出现了几次，因为不论是0次还是2次都是不计入答案的，所以只要把2次当0次看就可以避免很多复杂的讨论了。然后修改的时候tag是0就加，tag是1就减，最后要把tag进行变换（即0->1，1->0）。

要说修改与mex这两个的话，还是看上面的讲解吧。

再说起来，其实树上莫队可以在树上分块的基础上搞，但是我太蒻了，看不懂dalao的讲解。

还有一题：P4074 [WC2013]糖果公园

几乎就是板子吧，具体自己看代码（其实没啥差别）

手写AC（O2-6s，莫名其妙就Rank 5了）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
#include <bits/stdc++.h>
#define N 500000+100
using namespace std;
int n,m,blo,Time,tot,cur,q;
int a[N],in[N],dfn[N],bel[N],num[N],out[N],now[N];
int siz[N],deep[N],fa[N],son[N],p[N],top[N];
short tag[N];
long long Ans,ans[N],W[N],V[N];
struct node
{
    int l,r,tim,id,Lca;
}ask[N];
struct change
{
    int pos,New,Old;
}chg[N];
struct edge
{
    int to,nxt;
}e[N];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch>'9'||ch<'0')
    {
        if(f=='-')
            f=-1;
        ch=getchar();
    }
    while (ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline bool cmp(node x,node y)
{
    if(bel[x.l]==bel[y.l])
    {
        if(bel[x.r]==bel[y.r])
            return x.tim<y.tim;
        return bel[x.r]<bel[y.r];
    }
    return bel[x.l]<bel[y.l];
}
inline void add_edge(int u,int v)
{
    e[++tot]=(edge){v,p[u]};
    p[u]=tot;
}
inline void dfs(int x)
{
    siz[x]++;
    dfn[++dfn[0]]=x;
    in[x]=dfn[0];
    int f=-1;
    for(int i=p[x];i;i=e[i].nxt)
    {
        int v=e[i].to;
        if(v==fa[x])
            continue;
        deep[v]=deep[x]+1;
        fa[v]=x;
        dfs(v);
        siz[x]+=siz[v];
        if(siz[v]>f)
        {
            son[x]=v;
            f=siz[v];
        }
    }
    if(f==-1)
        son[x]=x;
    dfn[++dfn[0]]=x;
    out[x]=dfn[0];
}
inline int LCA(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(deep[top[x]]<deep[top[y]])
            swap(x,y);
        x=fa[top[x]];
    }
    if(deep[x]>deep[y])
        swap(x,y);
    return x;
}
inline void choose(int x,int y,int cur)
{
    int l=0,r=0,lca=LCA(x,y);
    if(x==lca||y==lca)
    {
        if(abs(in[x]-in[y])<abs(out[x]-out[y]))
            l=min(in[x],in[y]),r=max(in[x],in[y]);
        else
            l=min(out[x],out[y]),r=max(out[x],out[y]);
        lca=0;
    }
    else
    {
        if(abs(in[x]-out[y])<abs(out[x]-in[y]))
            l=min(in[x],out[y]),r=max(in[x],out[y]);
        else
            l=min(out[x],in[y]),r=max(out[x],in[y]);
    }
    ask[cur]=(node){l,r,Time,cur,lca};
}
inline void add(int x)
{
    num[x]++;
    Ans+=W[num[x]]*V[x];
}
inline void Minus(int x)
{
    Ans-=W[num[x]]*V[x];
    num[x]--;
}
inline void Work(int x)
{
    if(tag[x])
        Minus(a[x]);
    else
        add(a[x]);
    tag[x]^=1;
}
inline void Change(int pos,int x)
{
    if(tag[pos])
    {
        Work(pos);
        a[pos]=x;
        Work(pos);
    }
    else
        a[pos]=x;
}
int main()
{
    n=read(),m=read(),q=read();
    blo=pow(n<<1,2.0/3)*0.7;
    for(register int i=1;i<=m;i++)
        V[i]=read();
    for(register int i=1;i<=n;i++)
        W[i]=read();
    for(register int i=1;i<n;i++)
    {
        int x,y;
        x=read(),y=read();
        add_edge(x,y),add_edge(y,x);
    }
    dfs(1);
    for(register int i=1;i<=n;i++)
        now[i]=a[i]=read();
    for(register int i=1;i<=dfn[0];i++)
    {
        bel[i]=i/blo;
        if(top[dfn[i]])
            continue;
        else if(dfn[i]==son[fa[dfn[i]]])
            top[dfn[i]]=top[fa[dfn[i]]];
        else
            top[dfn[i]]=dfn[i];
    }
    for(register int i=1;i<=q;i++)
    {
        int c=read();
        if(c)
        {
            int x=read(),y=read();
            choose(x,y,++cur);
        }
        else
        {
            int x=read(),y=read();
            chg[++Time]=(change){x,y,now[x]};
            now[x]=y;
        }
    }
    sort(ask+1,ask+1+cur,cmp);
    int L=1,R=0,T=0;
    for(register int i=1;i<=cur;i++)
    {
        while(T<ask[i].tim)
        {
            T++;
            Change(chg[T].pos,chg[T].New);
        }
        while(T>ask[i].tim)
        {
            Change(chg[T].pos,chg[T].Old);
            T--;
        }
        while(L>ask[i].l)
        {
            L--;
            Work(dfn[L]);
        }
        while(R<ask[i].r)
        {
            R++;
            Work(dfn[R]);
        }
        while(L<ask[i].l)
        {
            Work(dfn[L]);
            L++;
        }
        while(R>ask[i].r)
        {
            Work(dfn[R]);
            R--;
        }
        if(ask[i].Lca)
            Work(ask[i].Lca);
        ans[ask[i].id]=Ans;
        if(ask[i].Lca)
            Work(ask[i].Lca);
    }
    for(register int i=1;i<=cur;i++)
        printf("%lld\n",ans[i]);
    return 0;
}

以上就是莫队——一个优雅的暴力算法

0%