在图中,有这样一类问题:在一张有向图中,指定源点S和汇点T,每条边的最大容量已知,求从S到T的最大流量。
这就是网络最大流问题,我们可以说的具体一点:一个自来水管道网,你家是汇点,自来水厂是源点,每根管道的粗细是一定的,求能流到你家的水最多有多少。
这个问题的关键在于,当有找到一条路径的时候,这条路径所经过的边的容量就会被占用一部分。
我们定义:
源点:只有流出去的点
汇点:只有流进来的点
流量:一条边上流过的流量
容量:一条边上可供流过的最大流量
残量:一条边上的容量-流量
模板题:P3376 【模板】网络最大流
我在这里介绍以下几种算法:
1、Edmond-Karp(EK)动能算法
EK这东西比较的简单粗暴,但复杂度是平方级别的O($m^2n$),所以跑的比较慢
首先我们说如果所有边上的流量都没有超过容量(不大于容量),那么就把这一组流量,或者说,这个流,称为一个可行流。一个最简单的例子就是,零流,即所有的流量都是0的流。
我们就从这个零流开始考虑,假如有这么一条路,这条路从源点开始一直一段一段的连到了汇点,并且,这条路上的每一段都满足流量<容量,注意,是严格的<,而不是<=。那么,我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta,一定可以保证这个流依然是可行流,这是显然的。
这样我们就得到了一个更大的流,他的流量是之前的流量+delta,而这条路就叫做增广路。
我们不断地从起点开始寻找增广路,每次都对其进行增广,直到源点和汇点不连通,也就是找不到增广路为止。当找不到增广路的时候,当前的流量就是最大流,这个结论非常重要。
那么我们寻找增广路的时候就简单的从源点开始做bfs,不断的修改这条路上的delta值,直到找到源点或找不到增广路。
但是这样会出一点锅,为什么呢?
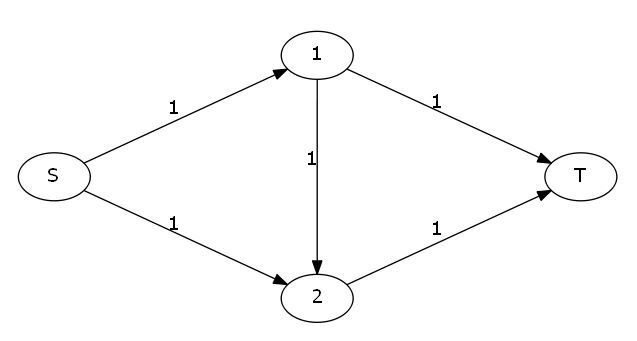
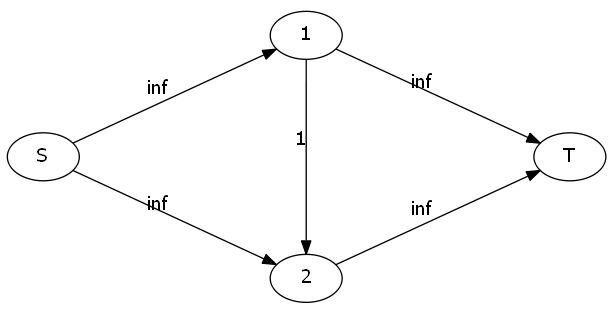
来看下面这张图:
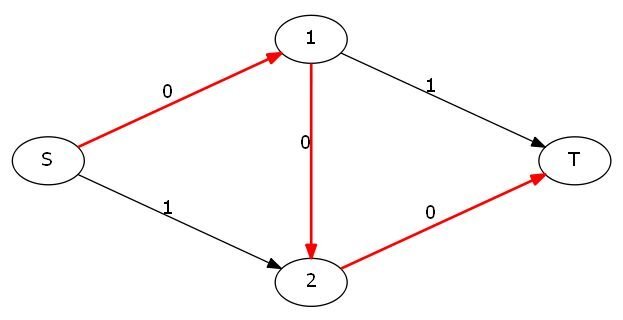
这个图我们一看就知道正确的方法是S-1-T和S-2-T,最大流就是2。但如果你的程序走过了S-1-2-T这条路,图就变成了这样:
这样源点与汇点就不连通了,但此时毫无疑问并不是最大值。那么该怎么办呢?我们可以考虑加入反向边,反向边初始容量都为0,然后在一条边的容量减少delta的时候把反向边的容量加上delta。
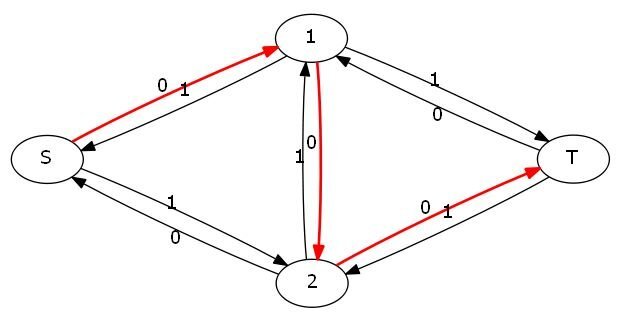
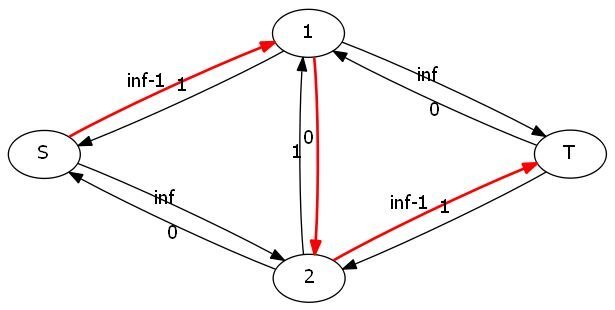
就拿上面那个图来说,加入反向边以后图就变成了这样:
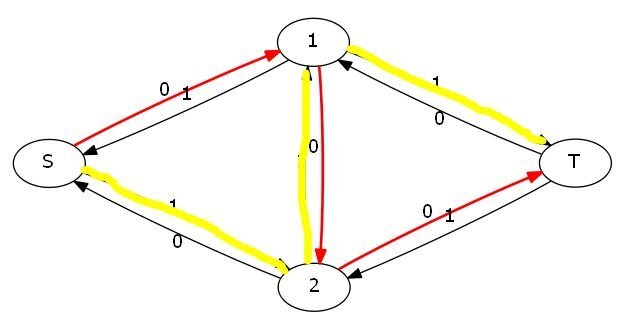
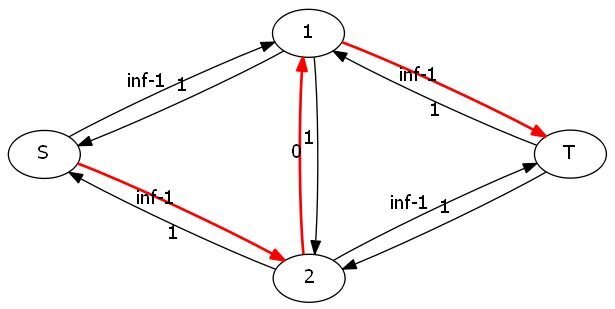
然后就可以搜到这样一条路(亮瞎眼的那条黄色路径):
这样就可以得到2的正确答案了。
那么这样为什么是对的呢?很简单,走2-1的时候就相当于把1-2这条边已经走的退了回去,这样就又变成了S-1-T和S-2-T两条路了。这样就给了程序一个反悔的机会。
然后就完了DA☆ZE!
贴代码(236ms):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
using namespace std;
int n,m,S,T,cnt,ans;
int head[N],q[N],pre[N];
bool vis[N];
struct edge
{
int fr,to,nxt,weigh;
}e[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
inline int add(int u,int v,int w)
{
e[cnt]=(edge){u,v,head[u],w};
head[u]=cnt++;
}
inline bool bfs(int s,int t)
{
memset(vis,0,sizeof(vis));
memset(pre,-1,sizeof(pre));
int fr=1,tl=0;
q[1]=s,vis[s]=1;
while(tl<fr)
{
int u=q[++tl];
for(register int i=head[u];i!=-1;i=e[i].nxt)
{
int v=e[i].to;
if(!vis[v]&&e[i].weigh>0)
{
pre[v]=i;
vis[v]=1;
if(v==t)
return true;
q[++fr]=v;
}
}
}
return false;
}
inline int EK(int s,int t)
{
int mn;
while(bfs(s,t))
{
mn=0x7fffffff;
int i=pre[t];
while(i!=-1)
{
mn=min(mn,e[i].weigh);
i=pre[e[i].fr];
}
i=pre[t];
while(i!=-1)
{
e[i].weigh-=mn;
e[i^1].weigh+=mn;
i=pre[e[i].fr];
}
ans+=mn;
}
return ans;
}
int main()
{
memset(head,-1,sizeof(head));
n=read(),m=read(),S=read(),T=read();
for(register int i=1;i<=m;i++)
{
int u,v,w;
u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,0);
}
printf("%d",EK(S,T));
return 0;
}
pre数组的作用是记录到达每个顶点的边。
【注明】本段讲解部分引用最大流模板【EdmondsKarp算法,简称EK算法,O(m^2n)】
2、Dinic算法
这个算法的复杂度为O($n^2m$),虽然仍旧是平方级别,但由于点的数量一般比边的数量少,所以整体比EK跑的要快。
普通Dinic
由于EK算法本身的特性,如果之前那张图变成了这样:
情况就很不乐观了。因为一次增广后图变成这样:
然后再BFS一次:
就这么做下去的话毫无疑问会爆炸的。
所以我们在这里引入一个分层图的概念。对于每一个点,我们根据从源点开始的BFS序列确定其深度,然后进行若干次DFS寻找增广路,每次由u推出的点v的深度必须是u的深度+1,这样就可以达到分层的效果。
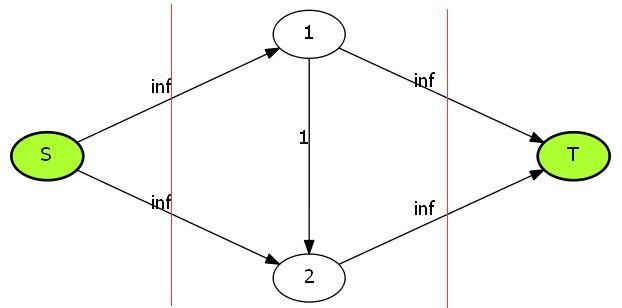
比如说还是上面那张图,它分层后就是这样:
然后很明显1和2这两个点在同一深度,它们在DFS中是无法互相搜到的。
至于BFS过程本身的变化其实不是特别大,对于一个点v进队的条件,不过是从EK的“当前边的残量大于0”变成了“当前边的残量大于0且v点未分配深度”而已,如果v没有分配深度,就把它的深度赋为u的深度+1。
然后在Dinic的主过程中就只需要不停的寻找增广路知道再也找不到为止。
以下是代码(手写520ms):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
using namespace std;
int n,m,S,T,cnt;
int deep[N/10],head[N],q[N/10];
struct edge
{
int to,nxt,weigh;
}e[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
inline void add(int u,int v,int w)
{
e[cnt]=(edge){v,head[u],w};
head[u]=cnt++;
}
inline bool bfs(int s,int t)
{
int fr=1,tl=0;
memset(deep,0,sizeof(deep));
deep[s]=1;
q[1]=s;
while(tl<fr)
{
int u=q[++tl];
for(register int i=head[u];i!=-1;i=e[i].nxt)
{
int v=e[i].to;
if(deep[v]==0&&e[i].weigh>0)
{
deep[v]=deep[u]+1;
q[++fr]=v;
}
}
}
if(!deep[t])
return 0;
return 1;
}
inline int dfs(int u,int t,int dist)
{
if(u==t)
return dist;
for(register int i=head[u];i!=-1;i=e[i].nxt)
{
int v=e[i].to;
if(deep[v]==deep[u]+1&&e[i].weigh>0)
{
int dis=dfs(v,t,min(dist,e[i].weigh));
if(dis>0)
{
e[i].weigh-=dis;
e[i^1].weigh+=dis;
return dis;
}
}
}
return 0;
}
inline int Dinic(int s,int t)
{
int Ans=0;
while(bfs(s,t))
{
while(int delta=dfs(s,t,inf))
Ans+=delta;
}
return Ans;
}
int main()
{
memset(head,-1,sizeof(head));
n=read(),m=read(),S=read(),T=read();
for(register int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,0);
}
printf("%d",Dinic(S,T));
return 0;
}
当前弧优化的Dinic
如果你比较细心的话大概就会注意到,EK的时间是236ms,而Dinic却要520ms。可这不对啊,说好的EK复杂度更高呢?原因就在于数据太水每次搜的时候都是从第一条边开始的,然后就导致有许多边被重复搜索,就跑得很慢啦。
那么我们就记录u之前循环到了哪条边然后直接从这条边开始不就完了吗?
对,就是这样,只要多开一个cur数组记录一下就行了,然后在DFS的循环中i改变的时候也同时改变cur来记录当前弧,但是不要忘记每一次建立完分层图后都要把cur置为每一个点的第一条边。
然后就可以跑的很快了DA☆ZE!
贴代码(手写132ms):1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
using namespace std;
int n,m,S,T,cnt;
int deep[N/10],head[N],q[N/10],cur[N];
struct edge
{
int to,nxt,weigh;
}e[N];
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x*f;
}
inline void add(int u,int v,int w)
{
e[cnt]=(edge){v,head[u],w};
head[u]=cnt++;
}
inline bool bfs(int s,int t)
{
int fr=1,tl=0;
memset(deep,0,sizeof(deep));
deep[s]=1;
q[1]=s;
while(tl<fr)
{
int u=q[++tl];
for(register int i=head[u];i!=-1;i=e[i].nxt)
{
int v=e[i].to;
if(deep[v]==0&&e[i].weigh>0)
{
deep[v]=deep[u]+1;
q[++fr]=v;
}
}
}
if(!deep[t])
return 0;
return 1;
}
inline int dfs(int u,int t,int dist)
{
if(u==t)
return dist;
for(register int& i=cur[u];i!=-1;i=e[i].nxt)//当然也可以去掉‘&’然后在循环最后加一句“cur[u]=e[i].nxt”
{
int v=e[i].to;
if(deep[v]==deep[u]+1&&e[i].weigh>0)
{
int dis=dfs(v,t,min(dist,e[i].weigh));
if(dis>0)
{
e[i].weigh-=dis;
e[i^1].weigh+=dis;
return dis;
}
}
}
return 0;
}
inline int Dinic(int s,int t)
{
int Ans=0;
while(bfs(s,t))
{
for(register int i=1;i<=n;i++)
cur[i]=head[i];
while(int delta=dfs(s,t,inf))
Ans+=delta;
}
return Ans;
}
int main()
{
memset(head,-1,sizeof(head));
n=read(),m=read(),S=read(),T=read();
for(register int i=1;i<=m;i++)
{
int u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,0);
}
printf("%d",Dinic(S,T));
return 0;
}
然后我们就得到了真正的Dinic算法
【注明】本段讲解部分引用SYCstudio大佬的Dinic算法(研究总结,网络流)