最短路

Posted on | In |
Words count in article: 2.2k | Reading time ≈ 11

如标题所示，这一类的算法就是为了解决这一类的单源最短路径问题。

所谓的单源最短路径问题呢，就是指在一个有向图中，给定点S，要求从S点出发遍历全图的最短路径。

例题：P3371 【模板】单源最短路径

以下我来讲几种算法（如果有可能的话）

1、SPFA

它被誉为“最快最好用的最短路算法”，但是被各种心狠手辣的出题人卡成了狗自有其优越性，毕竟像笔者这种蒟蒻都看了一遍就懂了。

SPFA用了一种动态逼近的方法，设立一个先进先出的队列q来保存待优化的节点，每次取出队首的节点u，并用u点当前的最短路径的估计值对离开u指向的v节点进行松弛操作，如果v点的最短路径估计值有所调整，并且v不在当前队列中，就把它放入队列中如此不断从队列中取出节点进行松弛操作，直至队列空为止。

那么说到松弛操作，原理就是十分著名的三角不等式，即我们数学中都用过的“两边之和大于第三边”，也就是v当前的最短路径估算值大于u当前的最短路径估算值与边[u,v]的长度之和，那么就更新v最短路径的估算值，也就是这样：

1
2
if(dist[v]>dist[u]+e[i].weigh)
	dist[v]=dist[u]+e[i].weigh;

当然，实际的代码中还要加上进队的操作。

当然你也许会说，这个怎么这么像BFS呢？其实还真有点，区别就在于BFS中一个点不能重复进队，而这里是可以反复松弛的。

切记：每次取出队首节点的时候一定要清空标记！！

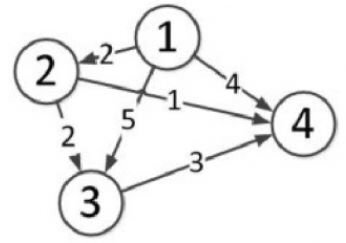
那么在贴代码之前，先来手玩一下样例。样例图如下：

过程如下：

Array 1 2 3 4
q 1 - - -
dis 0 inf inf inf

源点1进队，更新最短距离

Array 1 2 3 4
q 2 3 4 -
dis 0 2 5 4

1出队，2、3、4进队，2<inf，5<inf，4<inf，更新2、3、4的最短路径

Array 1 2 3 4
q 3 4 - -
dis 0 2 4 3

2出队，5>2+2，4>2+1，更新3、4的最短路径

Array 1 2 3 4
q 4 - - -
dis 0 2 4 3

3出队

Array 1 2 3 4
q - - - -
dis 0 2 4 3

4出队，队列已空，此时已找到最短路径

以下是代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <bits/stdc++.h>
#define N 1000000+110
#define inf 0x7fffffff
using namespace std;
int n,m,S,cnt;
int dist[N],head[N],q[N];
bool vis[N];
struct edge
{
    int to,nxt,weigh;
}e[N];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline void add(int u,int v,int w)
{
    e[++cnt]=(edge){v,head[u],w};
    head[u]=cnt;
}
inline void SPFA(int s)
{
    int fr=1,tl=0;
    for(int i=1;i<=n;i++)
        dist[i]=inf,vis[i]=0;
    dist[s]=0;
    q[1]=s;
    vis[s]=1;
    while(tl<fr)
    {
        int u=q[++tl];
        vis[u]=0;
        for(register int i=head[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(dist[v]>dist[u]+e[i].weigh)
            {
                dist[v]=dist[u]+e[i].weigh;
                if(!vis[v])
                {
                    q[++fr]=v;
                    vis[v]=1;
                }
            }
        }
    }
}
int main()
{
    n=read(),m=read(),S=read();
    for(register int i=1;i<=m;i++)
    {
        int u=read(),v=read(),w=read();
        add(u,v,w);
    }
    SPFA(S);
    for(register int i=1;i<=n;i++)
        printf("%d ",dist[i]);
    return 0;
}

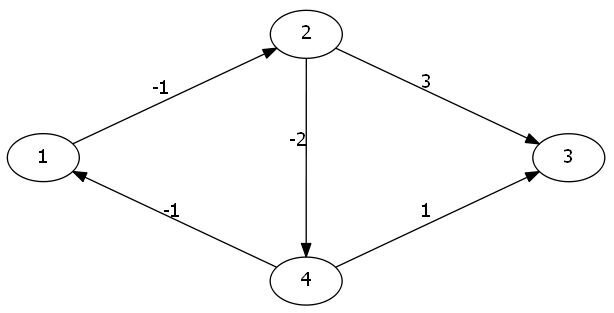
虽然这样写基本正确，但如果面对这样一个图，SPFA就很绝望了：

可以看到，1、2、4三点间形成了一个负环，也就是说这几个点间没有所谓的最短路，因此就会无限的跑下去。

那么怎么办呢？我们可以对每个点入队的次数进行限制，如果超过所有点的总数，那么就可以判断出现了负环，就跳出函数。

代码也没有太大的区别：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
inline void SPFA(int s)
{
    int fr=1,tl=0;
    for(int i=1;i<=n;i++)
        dist[i]=inf,vis[i]=0,c[i]=0;
    dist[s]=0;
    q[1]=s;
    vis[s]=1;
    while(tl<fr)
    {
        int u=q[++tl];
        vis[u]=0;
        for(register int i=head[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(dist[v]>dist[u]+e[i].weigh)
            {
                dist[v]=dist[u]+e[i].weigh;
                if(!vis[v])
                {
                    q[++fr]=v;
                    c[v]++;
                    vis[v]=1;
                    if(c[v]>n)
                        do something,return;
                }
            }
        }
    }
}

还有另一种办法，就是使用DFS跑SPFA，但是会稍微慢一点……吧

但是优点是负环的判断很简单，只要松弛了未清除标记的点就判定为出现负环。

下面是P3385 【模板】负环的代码（才不是跑P3371的时候T掉了呢，哼！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <bits/stdc++.h>
#define N 1000000+110
#define inf 0x7fffffff
using namespace std;
int n,m,S,cnt;
int dist[N],head[N],q[N];
bool vis[N],flag;
struct edge
{
    int to,nxt,weigh;
}e[N];
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline void add(int u,int v,int w)
{
    e[++cnt]=(edge){v,head[u],w};
    head[u]=cnt;
}
inline void SPFA(int u)
{
    vis[u]=1;
    for(register int i=head[u];i;i=e[i].nxt)
    {
        int v=e[i].to;
        if(dist[v]>dist[u]+e[i].weigh)
        {
            dist[v]=dist[u]+e[i].weigh;
            if(vis[v]||flag)
            {
                flag=1;
                break;
            }
            SPFA(v);
        }
    }
    vis[u]=0;
}
int main()
{
    int T=read();
    while(T--)
    {
        n=read(),m=read();
        for(register int i=1;i<=n;i++)
            dist[i]=0,vis[i]=0,head[i]=0;
        flag=0,cnt=0;
        for(register int i=1;i<=m;i++)
        {
            int u=read(),v=read(),w=read();
            add(u,v,w);
            if(w>0)
                add(v,u,w);
        }
        for(register int i=1;i<=n;i++)
        {
            SPFA(i);
            if(flag)
                break;
        }
        if(flag)
            printf("YE5\n");
        else
            printf("N0\n");
    }
    return 0;
}

再放一道例题：P1027 Car的旅行路线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
#include <bits/stdc++.h>
#define N 400+10
#define inf 0x7fffffff
#define ri register int
#define il inline
using namespace std;
int n,s,t,A,B,cnt,head[N],q[N];
double dist[N];
bool vis[N];
struct Vector
{
    int x,y;
    Vector(int X,int Y)
    {
        x=X,y=Y;
    }
    Vector()
    {
        x=0,y=0;
    }
    int operator * (const Vector &v)
    {
        int ret;
        ret=x*v.x+y*v.y;
        return ret;
    }
    Vector operator - (const Vector &v)
    {
        Vector ret;
        ret.x=x-v.x;
        ret.y=y-v.y;
        return ret;
    }
};
struct city
{
    Vector apt[5];
    int T;
    void add(int x1,int y1,int x2,int y2,int x3,int y3,int x4,int y4,int t)
    {
        apt[1].x=x1,apt[1].y=y1,apt[2].x=x2,apt[2].y=y2,apt[3].x=x3,apt[3].y=y3,apt[4].x=x4,apt[4].y=y4;
        T=t;
    }
};
struct edge
{
    int to,nxt;
    double weight;
};
city C[N];
edge e[100000];
il void work(int x1,int y1,int x2,int y2,int x3,int y3,int &x4,int &y4)
{
    Vector ab(x1-x2,y1-y2),bc(x2-x3,y2-y3),ac(x3-x1,y3-y1);
    if(ab*bc==0)
    {
        x4=x3+x1-x2;
        y4=y3+y1-y2;
    }
    else if(ab*ac==0)
    {
        x4=x3+x2-x1;
        y4=y3+y2-y1;
    }
    else
    {
        x4=x1+x2-x3;
        y4=y1+y2-y3;
    }
    return;
}
il double Vector_module(Vector v)
{
    return sqrt(v.x*v.x+v.y*v.y);
}
il void add_edge(int u,int v,double w)
{
    e[++cnt]=(edge){v,head[u],w};
    head[u]=cnt;
}
il void SPFA(int S)
{
    int fr=4,tl=0;
    for(ri i=1;i<=s;i++)
        for(ri j=1;j<=4;j++)
            dist[4*(i-1)+j]=inf;
    for(ri i=0;i<4;i++)
        dist[S+i]=0,vis[S+i]=1,q[i+1]=S+i;
    while(tl<fr)
    {
        int u=q[++tl];
        vis[u]=0;
        for(ri i=head[u];i;i=e[i].nxt)
        {
            int v=e[i].to;
            if(dist[v]>dist[u]+e[i].weight)
            {
                dist[v]=dist[u]+e[i].weight;
                if(!vis[v])
                {
                    q[++fr]=v;
                    vis[v]=1;
                }
            }
        }
    }
}
int main()
{
    scanf("%d",&n);
    while(n--)
    {
        memset(vis,0,sizeof(vis));
        memset(e,0,sizeof(e));
        memset(C,0,sizeof(C));
        memset(head,0,sizeof(head));
        cnt=0;
        scanf("%d %d %d %d",&s,&t,&A,&B);
        for(ri i=1;i<=s;i++)
        {
            int x1,x2,x3,x4;
            int y1,y2,y3,y4;
            int T;
            scanf("%d %d %d %d %d %d %d",&x1,&y1,&x2,&y2,&x3,&y3,&T);
            work(x1,y1,x2,y2,x3,y3,x4,y4);
            C[i].add(x1,y1,x2,y2,x3,y3,x4,y4,T);
        }
        for(ri i=1;i<=s;i++)
        {
            for(ri j=1;j<=3;j++)
                for(ri k=j+1;k<=4;k++)
                {
                    double w=Vector_module(C[i].apt[j]-C[i].apt[k])*C[i].T;
                    add_edge(4*(i-1)+j,4*(i-1)+k,w);
                    add_edge(4*(i-1)+k,4*(i-1)+j,w);
                }
            for(ri j=i+1;j<=s;j++)
                for(ri k=1;k<=4;k++)
                    for(ri l=1;l<=4;l++)
                    {
                        double w=Vector_module(C[i].apt[k]-C[j].apt[l])*t;
                        add_edge(4*(i-1)+k,4*(j-1)+l,w);
                        add_edge(4*(j-1)+l,4*(i-1)+k,w);
                    }
        }
        SPFA(4*(A-1)+1);
        double ans=inf;
        for(ri i=1;i<=4;i++)
            ans=min(ans,dist[4*(B-1)+i]);
        printf("%.1lf\n",ans);
    }
    return 0;
}

0%