点分治学习笔记

Posted on | In |
Words count in article: 4k | Reading time ≈ 20

点分治学习笔记

什么是点分治

点分治是一种能够比较方便的处理树上的路径问题的工具，以下有一个简单的例子：

给出一棵n个节点的树和一个整数k，问树上距离是k的倍数的点对有多少。

一个显然的做法是暴力选择两个点，然后 $\text{DFS}$ 暴力找路径，复杂度 $O(n^3)$ 。

$n>1000$ ，哦豁完蛋。

记录每个到根的距离然后每次枚举点对的时候倍增/树剖求 $\text{LCA}$ ？

$n>10^4$ 后这种复杂度为 $O(n^2logn)$ 的做法也稳定TLE了，所以呢？

一种做法是找到一个根，然后遍历这个子树中的每个点，依次处理每个点的子树答案。

在子树里可以直接把所有点到根的路径长度对 $k$ 取模之后排序，然后就可以用乘法原理快速求出答案（

期望复杂度 $O(nklogn)$ （大概吧

为了实现上述做法就回到了这篇文章的话题：点分治。

点分治原理

接着上面的说法，我们可以想到对于一条路径，有且仅有以下两种情况：

  1. 在子树中，不经过根节点
  2. 从一棵子树跨过根节点到另外一棵子树

显然我们会发现：随着往下递归的进行，所有的情况1最后都会变成情况2，所以我们只用考虑这一种情况便好。然后我们又可以发现：在子树中只要记录每一个点到当前子树根节点的距离就可以算出任意两点间的路径长。

这就是分治的基本原理。

选择重心

说到底点分治还是分治，也就是简单的把问题分成几个子问题然后合并，但是怎么分与怎么合并，这些都是问题。

显然我们可以想到的是选择子树根节点的时候不能随便选，因为分治问题一般都是递归处理，所以说根的选择会涉及到递归深度的问题，于是就提到点分治中的一个概念：重心。我们把一棵无根树中那个作为根后可以使得最大的子树最小的点称为这棵树的重心。

求重心不是一个麻烦问题，树形 $\text{DP}$ 就能轻松解决，复杂度 $O(n)$ 。

以下是几个会用到的变量：

  • $siz[i]$ 以 $i$ 为根节点的子树的节点数
  • $sum$ 总结点数
  • $f[i]$ 以 $i$ 为根节点的所有子树中最大子树的 $siz$

然后由于并不复杂，代码很好读懂，我也就不解释了（懒.jpg

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
il void Get_Root(int x, int pre)
{
	siz[x] = 1, f[x] = 0;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (v == pre || vis[v])
			continue;
		Get_Root(v, x);
		siz[x] += siz[v];
		f[x] = chkmax(f[x], siz[v]);
	}
	f[x] = max(f[x], sum - siz[x]);
	if (f[x] < f[rt])
		rt = x;
}

点分治的实现

有了以上的东西之后，点分治就很好实现了

首先仍然是几个（其实只有一个）变量：

  • $vis[i]$ 用与记录节点 $i$ 是否被分治过

然后由于并不难理解，也直接放代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
il void Solve(int x)
{
	ans += calc(x, 0);
	vis[x] = 1;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v])
			continue;
		sum = f[0] = siz[v];
		rt = 0;
		Get_Root(v, x);
		Solve(rt);
	}
}

需要注意的是为了是每一次递归都是最优的，所以递归到下一层前需要先求出子树的重心。

另外，这里的 $calc$ 函数是一个统计答案的函数，因题而异。

而且由于题目的不同 $Solve$ 函数也会发生变化，所以这里记板子并没有什么作用。

关于统计答案发生错误的那档事

如果你按照上面的 $Solve$ 函数去打的话，你会发现答案是错的。为什么呢？其实我们仔细想一想就会发现问题了：

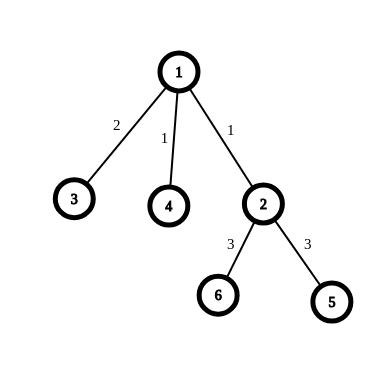
在上图中我们分治到节点1的子树后我们会认为节点5和节点6的距离是4+4=8，但这显然是错误的，所以在往下递归之前要把这些多算的东西减掉。

然后就变成了这样：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
il void Solve(int x)
{
	ans += calc(x, 0);
	vis[x] = 1;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v])
			continue;
        ans -= calc(x, G.e[i].weight)
		sum = f[0] = siz[v];
		rt = 0;
		Get_Root(v, x);
		Solve(rt);
	}
}

所以开头的那道例题

我就不讲了（反正都是我瞎yy的，我才懒得写呢

一些例题

1.【国家集训队】聪聪可可

题意

给出一棵树，问两个点之间的距离能被3整除的概率是多少

思路

显然是一道裸题，用t[i]表示子树中到根的距离模3为i的点对数量，显然在一棵子树中的答案就是

所以就只用DFS一遍就可以解决了

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
#include <bits/stdc++.h>
#define ri register int
#define il inline
using namespace std;

typedef long long ll;
typedef unsigned long long ull;

const int N = 1e6 + 110;
const int MAXN = 110;
const int inf = 0x7fffffff;
const double eps = 1e-8;

il int chkmax(int a, int b)
{
	return a > b ? a : b;
}
il int chkmin(int a, int b)
{
	return a < b ? a : b;
}

il int gcd(int a, int b)
{
	return b ? gcd(b, a % b) : a;
}

il int read()
{
	int x = 0, f = 1;
	char ch = getchar();
	while (!isdigit(ch))
	{
		if (ch == '-')
			f = -1;
		ch = getchar();
	}
	while (isdigit(ch))
	{
		x = (x << 3) + (x << 1) + ch - '0';
		ch = getchar();
	}
	return x * f;
}

int n, sum, rt, ans;
int siz[N], f[N], dep[N], t[3];
bool vis[N];

struct Graph
{
	int cnt, head[N];
	
	struct edge
	{
		int to, nxt, weight;
	};
	edge e[N];
	
	il void add_edge(int u, int v, int w)
	{
		e[++cnt] = (edge) {v, head[u], w};
		head[u] = cnt;
	}
	il void Link(int u, int v, int w)
	{
		add_edge(u, v, w);
		add_edge(v, u, w);
	}
};
Graph G;

il void Get_Root(int x, int pre)
{
	siz[x] = 1, f[x] = 0;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (v == pre || vis[v])
			continue;
		Get_Root(v, x);
		siz[x] += siz[v];
		f[x] = chkmax(f[x], siz[v]);
	}
	f[x] = max(f[x], sum - siz[x]);
	if (f[x] < f[rt])
		rt = x;
}

il void DFS(int x, int pre)
{
	t[dep[x]]++;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (v == pre || vis[v])
			continue;
		dep[v] = (dep[x] + G.e[i].weight) % 3;
		DFS(v, x);
	}
}

il int calc(int x, int now)
{
	memset(t, 0, sizeof(t));
	dep[x] = now;
	DFS(x, 0);
	return t[0] * t[0] + t[1] * t[2] * 2;
}

il void Solve(int x)
{
	ans += calc(x, 0);
	vis[x] = 1;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v])
			continue;
		ans -= calc(v, G.e[i].weight);
		sum = f[0] = siz[v];
		rt = 0;
		Get_Root(v, x);
		Solve(rt);
	}
}

int main()
{
	n = read();
	for (ri i = 1; i < n; i++)
	{
		int u = read(), v = read(), w = read();
		G.Link(u, v, w % 3);
	}
	rt = 0;
	sum = f[0] = n;
	Get_Root(1, 0);
	Solve(rt);
	int d = gcd(ans, n * n);
	printf("%d/%d", ans / d, n * n / d);
	return 0;
}
/*
5
1 2 1
1 3 2
1 4 1
2 5 3

*/

2.[POJ1741]Tree

题意

给出一棵树，问有多少点对的距离小于k

思路

在每一层分治的时候，记录一下每个点到当前重心的距离，然后双指针扫一下就完了

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
#include <bits/stdc++.h>
#define ri register int
#define il inline
using namespace std;

typedef long long ll;
typedef unsigned long long ull;

const int N = 1e6 + 110;
const int MAXN = 110;
const int inf = 0x7fffffff;
const double eps = 1e-8;

il int read()
{
	int x = 0, f = 1;
	char ch = getchar();
	while (!isdigit(ch))
	{
		if (ch == '-')
			f = -1;
		ch = getchar();
	}
	while (isdigit(ch))
	{
		x = (x << 3) + (x << 1) + ch - '0';
		ch = getchar();
	}
	return x * f;
}

il int chkmax(int a, int b)
{
	return a > b ? a : b;
}
il int chkmin(int a, int b)
{
	return a < b ? a : b;
}

int n, k, rt, sum, ans, tot;
int f[N], siz[N], dep[N], dis[N];
bool vis[N];

struct Graph
{
	int cnt, head[N];

	struct edge
	{
		int to, nxt, weight;
	};
	edge e[N];

	il void Clear()
	{
		cnt = 0;
		memset(head, 0, sizeof(head));
		memset(e, 0, sizeof(e));
	}

	il void add_edge(int u, int v, int w)
	{
		e[++cnt] = (edge) {v, head[u], w};
		head[u] = cnt;
	}
	il void Link(int u, int v, int w)
	{
		add_edge(u, v, w);
		add_edge(v, u, w);
	}
};
Graph G;

il void Clear()
{
	G.Clear();
	ans = 0;
	memset(vis, 0, sizeof(vis));
}

il void Get_Root(int x, int pre)
{
	siz[x] = 1, f[x] = 0;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (v == pre || vis[v])
			continue;
		Get_Root(v, x);
		siz[x] += siz[v];
		f[x] = chkmax(f[x], siz[v]);
	}
	f[x] = chkmax(f[x], sum - siz[x]);
	if (f[x] < f[rt])
		rt = x;
}

il void DFS(int x, int pre)
{
	dis[++tot] = dep[x];
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v] || v == pre)
			continue;
		dep[v] = dep[x] + G.e[i].weight;
		DFS(v, x);
	}
}

il int calc(int x, int now)
{
	tot = 0;
	dep[x] = now;
	DFS(x, 0);

	int ret = 0, l = 1, r = tot;
	sort(dis + 1, dis + 1 + tot);
	while(l < r)
	{
		while (dis[l] + dis[r] > k && l < r)
			r--;
		ret += r - l;
		l++;
	}
	return ret;
}

il void Solve(int x)
{
	ans += calc(x, 0);
	vis[x] = 1;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v])
			continue;
		ans -= calc(v, G.e[i].weight);
		sum = f[0] = siz[v];
		rt = 0;
		Get_Root(v, x);
		Solve(rt);
	}
}

int main()
{
	while (1)
	{
		n = read(), k = read();
		if (!n && !k)
			break;
		Clear();
		for (ri i = 1; i < n; i++)
		{
			int u = read(), v = read(), w = read();
			G.Link(u, v, w);
		}
		sum = f[0] = n;
		rt = 0;
		Get_Root(1, 0);
		Solve(rt);
		printf("%d\n", ans);
	}
	return 0;
}
/*
5 4
1 2 3
1 3 1
1 4 2
3 5 1
7 10
1 6 13 
6 3 9 
3 5 7 
4 1 3 
2 4 20 
4 7 2
0 0

*/

3.[Luogu3806]【模板】点分治1

题意

给出一棵树，问是否有距离为k的点对

题解

每一层分治的时候处理出子树中每个点到当前中心的距离，然后暴力枚举子树中的所有点对统计即可，最后查询的时候看距离为k的点对数量是否大于0即可

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
#include <bits/stdc++.h>
#define ri register int
#define il inline
using namespace std;

typedef long long ll;
typedef unsigned long long ull;

const int N = 1e6 + 110;
const int MAXN = 110;
const int inf = 0x7fffffff;
const double eps = 1e-8;

il int read()
{
	int x = 0, f = 1;
	char ch = getchar();
	while (!isdigit(ch))
	{
		if (ch == '-')
			f = -1;
		ch = getchar();
	}
	while (isdigit(ch))
	{
		x = (x << 3) + (x << 1) + ch - '0';
		ch = getchar();
	}
	return x * f;
}

il int chkmax(int a, int b)
{
	return a > b ? a : b;
}
il int chkmin(int a, int b)
{
	return a < b ? a : b;
}

int n, m, rt, tot, sum;
int siz[N], f[N], dep[N], ans[N], dis[N];
bool vis[N];

struct Graph
{
	int cnt, head[N];

	struct edge
	{
		int to, nxt, weight;
	};
	edge e[N];

	il void add_edge(int u, int v, int w)
	{
		e[++cnt] = (edge) {v, head[u], w};
		head[u] = cnt;
	}
	il void Link(int u, int v, int w)
	{
		add_edge(u, v, w);
		add_edge(v, u, w);
	}
};
Graph G;

il void Get_Root(int x, int pre)
{
	siz[x] = 1, f[x] = 0;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (v == pre || vis[v])
			continue;
		Get_Root(v, x);
		siz[x] += siz[v];
		f[x] = chkmax(f[x], siz[v]);
	}
	f[x] = chkmax(f[x], sum - siz[x]);
	if (f[x] < f[rt])
		rt = x;
}

il void DFS(int x, int pre)
{
	dis[++tot] = dep[x];
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v] || v == pre)
			continue;
		dep[v] = dep[x] + G.e[i].weight;
		DFS(v, x);
	}
}

il void calc(int x, int now, int QwQ)
{
	tot = 0;
	dep[x] = now;
	DFS(x, 0);

	for (ri i = 1; i <= tot; i++)
		for (ri j = 1; j <= tot; j++)
			if (i != j)
				ans[dis[i] + dis[j]] += QwQ;
}

il void Solve(int x)
{
	calc(x, 0, 1);
	vis[x] = 1;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v])
			continue;
		calc(v, G.e[i].weight, -1);
		sum = f[0] = siz[v];
		rt = 0;
		Get_Root(v, x);
		Solve(rt);
	}
}

int main()
{
	n = read(), m = read();
	for (ri i = 1; i < n; i++)
	{
		int u = read(), v = read(), w = read();
		G.Link(u, v, w);
	}
	sum = f[0] = n;
	rt = 0;
	Get_Root(1, 0);
	Solve(rt);
	for (ri i = 1; i <= m; i++)
	{
		int k = read();
		puts(ans[k] ? "AYE" : "NAY");
	}
	return 0;
}
/*
2 1
1 2 2
2

*/

4.[FJOI2014]最短路径树问题

题意

给出一张图，问在它字典序最小的最短路径树上经过k个节点的最长路径的长度与条数

思路

SB拼板题，套一个Dijkstra板子和一个点分治的板子就完了

点分治的部分就是递归下去后记录一下当前深度的最长路径与条数再转移一下就行了

所以这其实是一道长链剖分习题.jpg

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
#include <bits/stdc++.h>
#define ri register int
#define il inline
#define mp make_pair
using namespace std;

typedef long long ll;
typedef unsigned long long ull;

const int maxn = 1e6 + 110;
const int maxm = 110;
const int inf = 0x7fffffff;
const double eps = 1e-8;

il int read()
{
	int x = 0, f = 1;
	char ch = getchar();
	while (!isdigit(ch))
	{
		if (ch == '-')
			f = -1;
		ch = getchar();
	}
	while (isdigit(ch))
	{
		x = (x << 3) + (x << 1) + ch - '0';
		ch = getchar();
	}
	return x * f;
}

il int chkmax(int a, int b)
{
	return a > b ? a : b;
}
il int chkmin(int a, int b)
{
	return a < b ? a : b;
}

int n, m, k, ans, ans2;

vector <pair <int, int> > vec[maxn];
pair <int, int> fr[maxn];

struct Graph
{
	int cnt, head[maxn];

	struct edge
	{
		int to, nxt, weight;
	};
	edge e[maxn];

	il void add_edge(int u, int v, int w)
	{
		e[++cnt] = (edge) {v, head[u], w};
		head[u] = cnt;
	}
	il void Link(int u, int v, int w)
	{
		add_edge(u, v, w);
		add_edge(v, u, w);
	}
};
Graph G;

int dis[maxn];

priority_queue <pair <int, int>, vector <pair <int, int> >, greater <pair<int, int> > > q;

il void Dijkstra(int s)
{
	for (ri i = 1; i <= n; i++)
		dis[i] = inf;
	dis[s] = 0;
	q.push(mp(dis[s], s));
	while (!q.empty())
	{
		int u = q.top().second, dist = q.top().first;
		q.pop();
		if (dist != dis[u])
			continue;
		for (ri i = 0; i < vec[u].size(); i++)
		{
			int v = vec[u][i].first, w = vec[u][i].second;
			if (dis[v] > dis[u] + w)
			{
				dis[v] = dis[u] + w;
				q.push(mp(dis[v], v));
				fr[v] = mp(u, w);
			}
			else if (dis[v] == dis[u] + w && u < fr[v].first)
				fr[v] = mp(u, w);
		}
	}
}

int tot, rt, sum;
int siz[maxn], f[maxn], dist[maxn], S[maxn], num[maxn];
bool vis[maxn];

il void Get_Root(int x, int pre)
{
	siz[x] = 1, f[x] = 0;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v] || v == pre)
			continue;
		Get_Root(v, x);
		siz[x] += siz[v];
		f[x] = chkmax(f[x], siz[v]);
	}
	f[x] = chkmax(f[x], sum - siz[x]);
	if (f[x] < f[rt])
		rt = x;
}

il void DFS(int x, int pre, int now)
{
	tot = chkmax(tot, now);
	if (now == k - 1)
	{
		if (ans == dist[x])
			ans2++;
		if (dist[x] > ans)
			ans2 = 1, ans = dist[x];
		return;
	}
	int temp = -1;
	if (S[k - 1 - now] != -1)
		temp = dist[x] + S[k - 1 - now];
	if (ans == temp)
		ans2 += num[k - 1 - now];
	if (temp > ans)
		ans2 = num[k - 1 - now], ans = temp;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v] || v == pre)
			continue;
		dist[v] = dist[x] + G.e[i].weight;
		DFS(v, x, now + 1);
	}
}

il void calc(int x, int pre, int now)
{
	if (now == k - 1)
		return;
	if (S[now] == dist[x])
		num[now]++;
	else
		S[now] = chkmax(S[now], dist[x]), num[now] = 1;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v] || v == pre)
			continue;
		calc(v, x, now + 1);
	}
}

il void Solve(int x)
{
	tot = 0;
	vis[x] = 1;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v])
			continue;
		dist[v] = G.e[i].weight;
		DFS(v, x, 1);
		calc(v, x, 1);
	}
	for(ri i = 1; i <= tot; i++)
		S[i] = -1, num[i] = 0;
	for (ri i = G.head[x]; i; i = G.e[i].nxt)
	{
		int v = G.e[i].to;
		if (vis[v])
			continue;
		f[0] = sum = siz[v];
		rt = 0;
		Get_Root(v, 0);
		Solve(rt);
	}
}

int main()
{
	n = read(), m = read(), k = read();
	for (ri i = 1; i <= m; i++)
	{
		int u = read(), v = read(), w = read();
		vec[u].push_back(mp(v, w));
		vec[v].push_back(mp(u, w));
	}
	for (ri i = 1; i <= n; i++)
		sort(vec[i].begin(), vec[i].end());
	Dijkstra(1);
	for (ri i = 2; i <= n; i++)
		G.Link(i, fr[i].first, fr[i].second);
	f[0] = sum = n;
	rt = 0;
	Get_Root(1, 0);
	for (ri i = 1; i <= n; i++)
		S[i] = -1;
	Solve(rt);
	printf("%d %d", ans, ans2);
	return 0;
}
/*
6 6 4
1 2 1
2 3 1
3 4 1
2 5 1
3 6 1
5 6 1

*/

咕咕咕

如果我做到什么有意思的点分题再更新（

0%