FFT（Fast Fourier Transformation，法法塔）学习笔记，高中生（指我）都看不懂的FFT！

Posted on | In |
Words count in article: 3k | Reading time ≈ 13

35470184_p0.jpg

快速傅里叶变换（FFT）学习笔记

前言

FFT （ Fast Fourier Transformation ）是离散傅氏变换（ DFT ）的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。这里仅讨论 FFT 在 OI 中的应用。

多项式

数学课上大家都学过多项式，对于定义就不多讲了，这里讲一下多项式的表示方法

系数表示法

我们用的最多的表示法，设 $A(n)$ 表示一个 $n - 1$ 次多项式

则 $A(x) = \sum \limits {i = 0} ^{n} a {i} \times x ^{i}$

利用这种表示法计算多项式乘法是我们数学课上经常干的事情（不管你有没有意识到），但其实这只是一个 $O(n ^{2})$ 的暴力做法

点值表示法

我们数学课上不会用它去表示一个多项式，但是其思路我们是知道的

我们将多项式看做一个函数，那么任意选出 $n$ 个互不相同的值带进去就会有 $n$ 个不同的函数值，对应到坐标平面上就会有 $n$ 个点，该多项式可由这 $n$ 个点唯一确定。

然后我们惊奇地发现这样表示下的两个多项式相乘的复杂度是 $O(n)$ 的，比上面一种要优秀很多。

但是很遗憾，由于大多数题目给出的多项式都是系数表示的，要将其转化为点值表示再运算并最后转换回去，复杂度还是 $O(n ^2 )$ 的。

至此我们发现多项式的两种表示方法做多项式乘法都是 $O(n ^2 )$ 的，于是我们考虑进行优化。

复数

在谈优化之前，我们先岔开一下话题，谈一下复数

然后在介绍复数之前我们再先来谈一些可能会用到的东西

向量

具有大小和方向的量，几何中常用带有箭头的线段表示，其余见高中数学课本

向量的表示方法： $\vec{a}$ 或 $\boldsymbol{a}$ 均表示向量

圆的弧度制

将等于半径长的圆弧所对的圆心角叫做 1 弧度的角，符号为 rad ，用弧度作单位来度量角的制度为弧度制，与角度制相对，其余见高中数学课本

平行四边形定则

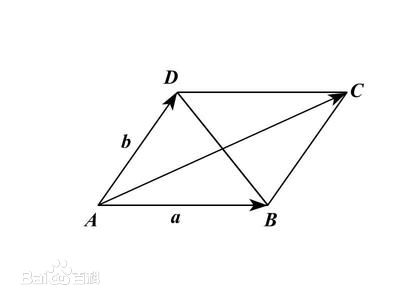
向量加法法则：即 $\vec {AC} = \boldsymbol{a} + \boldsymbol{b}$

下面我们正式开始讲复数。

复数的定义

初中老师会告诉我们复数是不能开根号的，但是高中老师就会告诉我们 $i = \sqrt{-1}$ ，我们把 $i$ 就叫做虚数单位，对于实数 $a, b$ ，形如 $a + bi$ 的数我们就称其为复数，其中 $a$ 为 实部 ， $bi$ 为 虚部 。可以简单地把复数理解为实部与虚部复合而成的数。

在复平面中， $x$ 轴代表实数， $y$ 轴（处原点以外）代表虚数，则在复平面上的向量 $(a, b)$ 就可以表示复数 $a + bi$ 。

模长：与向量的模长定义相同，即为 $\sqrt{a ^2 + b ^2 }$

幅角：为向量与 $x$ 轴正方向 的有向夹角，以逆时针为正方向，关于任意角的定义参见高中数学必修四

运算法则

加法

由于在复平面中复数可被表示为向量，所以复数的加法法则与向量加法法则相同。

乘法

几何意义：两向量模长相乘，幅角相加

代数意义：

单位根

从这里开始，无特殊说明均认为 $n$ 是 2 的整数次幂

定义

在复平面上，以原点为圆心， 1 为半径作出 单位圆 ，以原点为七点，圆的 $n$ 等分点为终点作出 $n$ 个向量，设幅角为正且最小的向量对应的复数为 $\omega _n$ ，称为 $n$ 次单位根。

根据复数乘法的运算法则，其余 $n - 1$ 个复数为 $\omega {n} ^{2},\ \omega {n} ^{3},\ …\ ,\ \omega _{n} ^{n}$

可知 $\omega {n} ^{0} = \omega {n} ^{n} = 1$ ，它们均对应复平面上 $x$ 轴正方向上的向量。

由欧拉公式可以计算出任意 $\omega _{n} ^{k}$ 的值

在代数中，若 $z ^{n} = 1$ ，我们就称 $z$ 为 $n$ 次单位根

性质

  • $\omega _{n} ^{k} = \cos{(k \frac{2\pi}{n})} + i \sin{(k \frac{2\pi}{n})}$ ，即欧拉公式

  • $\omega {2n} ^{2k} = \omega {n} ^{k}$

    证明：

  • $\omega {n} ^{k + \frac{n}{2}} = -\omega {n} ^{k}$

    证明：

  • $\omega {n} ^{0} = \omega {n} ^{n} = 1$

直到这里，我们和这篇文章的话题依然没有多大的关系，所以，前方高能预警，公式恐惧症患者请迅速撤离！

快速傅里叶变换

我们前面提到过，一个 $n$ 次多项式可以被 $n$ 个点唯一确定。

那么既然这 $n$ 个点是可以任意选定的，我们当然可以钦定它们为单位根的 0 到 $n - 1$ 次幂，然而这样复杂度并没有降低

我们设多项式 $A(x)$ 的系数为 $(a0,\ a_1,\ a_2,\ …\ ,\ a{n - 1})$ ，那么

将其下标按奇偶性分类

设

那么我们可以得到

我们将 $\omega_{n}^{k}\ (k\leq \frac{n}{2})$ 代入得

同理，我们将 $\omega _{n} ^{k + \frac{n}{2}}$ 代入得

两个式子一比较，我们发现它们只有一个常数项不同，也就是说我们枚举第一个式子的时候可以 $O(1)$ 的得到第二个式子

然后又发现当第一个式子的 $k$ 在 $[0, \frac{n}{2} - 1]$ 中取值的时候， $k + \frac{n}{2}$ 能取到 $[\frac{n}{2},\ n - 1]$ 中的每一个值

于是问题规模缩小了一半

而缩小后的问题仍然满足原问题的性质，于是我们可以递归的去搞直到多项式仅剩一个常数项

时间复杂度：不难看出 FFT 其实是一个分治算法，因此复杂度为 $O(nlogn)$

快速傅里叶逆变换

我们前面也提到过，大多数时候我们的多项式都是系数表示的，而 FFT 并不能解决多项式乘法的问题，它只是快速的把系数表示的多项式转换成了点值表示的多项式，而算出结果后我们还要把它转换回来，这里就要用到 傅里叶逆变换 。

设 $(y{0}, y{1}, y{2}, …, y{n - 1})$ 为 $(a{0}, a{1}, a{2}, …, a{n - 1})$ 的傅里叶变换（即点值表示）

假设有另一个向量 $(c{0}, c{1}, c{2}, …, c{n - 1})$ 为多项式 $B(x) = y {0} + y {1} x + y {2} x ^{2} + … + y {n - 1} x ^{n - 1}$ 在 $\omega {n} ^{0}, \omega {n} ^{-1}, \omega {n} ^{-2}, …, \omega {n} ^{-(n - 1)}$ 处的点值表示，即满足

然后继续推式子：

设 $S(x) = \sum \limits {i = 0} ^{n - 1} x ^{i}$ ， 将 $\omega {n} ^{k}$ 代入得

当 $k \not = 0$ 时，由等比数列求和公式（虽然 $\omega _{n} ^{k}$ 不为实数）可得

当 $k = 0$ 时，观察可得 $S(\omega _{n} ^{0}) = n$

继续考虑刚才的东西： $c {k} = \sum \limits {j = 0} ^{n - 1} a {j} (\sum \limits {i = 0} ^{n - 1} (\omega _{n} ^{j - k}) ^{i})$

可以发现当 $j \not = k$ 时，右边的累和式值为 0 ；当 $j = k$ 时，累和式的值为 $n$

因此我们有

即

这样我们就能通过傅里叶变换实现傅里叶逆变换了。

非递归 FFT

有上面推出来的东西，我们可以写出递归版的 FFT ，但是递归在很多时候是不够优秀的，于是我们就要用到非递归的 FFT 。

首先放一张图

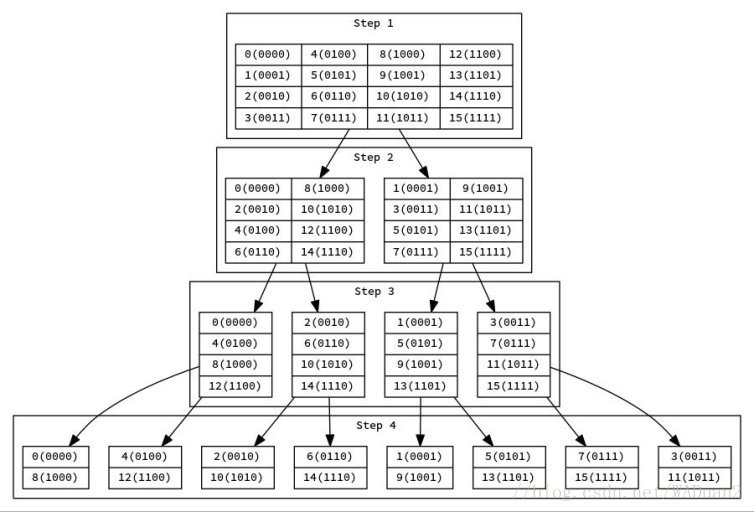
然后大家会发现：每个数最终的下标就是原下标二进制翻转之后的结果，那么我们就可以先把最终的序列弄出来，然后再向上合并

蝴蝶优化

由于笔者退役了，所以本部分无限期咕咕咕

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>
#define ri register int
#define il inline
#define elif else if
#define rep(i, j, k) for (ri (i) = (j); (i) <= (k); (i)++)
#define dep(i, j, k) for (ri (i) = (j); (i) >= (k); (i)--)
#define Side(x) for (ri i = head[(x)]; ~i; i = e[i].nxt)
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef complex <double> cpx;

const int maxn = 1e6 + 110;
const int N = 110;
const int inf = 0x7fffffff;
const double eps = 1e-8;
const double pi = acos(-1);

il int read() {
	int x = 0, f = 1;
	char ch = getchar();
	while (!isdigit(ch)) {
		if (ch == '-') f = -1;
		ch = getchar();
	}
	while (isdigit(ch)) {
		x = (x << 3) + (x << 1) + ch - '0';
		ch = getchar();
	}
	return x * f;
}

template <typename T>
il T chkmin(T a, T b) {return a < b ? a : b;}
template <typename T>
il T chkmax(T a, T b) {return a > b ? a : b;}

int n, m, lim;
int r[maxn];

il void init() {
	for (n = 1; n <= m; n <<= 1) lim++;
	rep(i, 0, n - 1) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (lim - 1));
}

il void FFT(cpx *a, int opt) {
	rep(i, 0, n - 1) if (i < r[i]) swap(a[i], a[r[i]]);
	for (ri i = 1; i < n; i <<= 1) {
		cpx W(cos(pi / i), opt * sin(pi / i));
		for (ri p = i << 1, j = 0; j < n; j += p) {
			cpx w(1, 0);
			for (ri k = 0; k < i; k++, w *= W) {
				cpx x = a[j + k], y = w * a[j + k + i];
				a[j + k] = x + y, a[j + k + i] = x - y;
			}
		}
	}
}

cpx a[maxn], b[maxn];

int main() {
	n = read(), m = read();
	rep(i, 0, n) a[i] = read();
	rep(i, 0, m) b[i] = read();
	m += n;
	init();
	FFT(a, 1), FFT(b, 1);
	rep(i, 0, n - 1) a[i] *= b[i];
	FFT(a, -1);
	rep(i, 0, m) printf("%d ", (int)(a[i].real() / n + 0.5));
	return 0;
}

后记

虽然早就写的差不多了，不过由于我比较颓，加上省选前的时间都用来打板子了，所以咕到现在才弄出来（虽然几乎都是抄的），然后本来还想再多学一点多项式相关的东西，结果退役了……

本博客大部分借鉴于

https://www.cnblogs.com/zwfymqz/p/8244902.html

图也全部都是盗的QwQ

0%